42. Trapping Rain Water #

题目 #

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

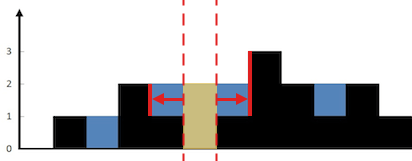
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

题目大意 #

从 x 轴开始，给出一个数组，数组里面的数字代表从 (0,0) 点开始，宽度为 1 个单位，高度为数组元素的值。如果下雨了，问这样一个容器能装多少单位的水？

解题思路 #

• 每个数组里面的元素值可以想象成一个左右都有壁的圆柱筒。例如下图中左边的第二个元素 1，当前左边最大的元素是 2 ，所以 2 高度的水会装到 1 的上面(因为想象成了左右都有筒壁)。这道题的思路就是左指针从 0 开始往右扫，右指针从最右边开始往左扫。额外还需要 2 个变量分别记住左边最大的高度和右边最大高度。遍历扫数组元素的过程中，如果左指针的高度比右指针的高度小，就不断的移动左指针，否则移动右指针。循环的终止条件就是左右指针碰上以后就结束。只要数组中元素的高度比保存的局部最大高度小，就累加 res 的值，否则更新局部最大高度。最终解就是 res 的值。
• 抽象一下，本题是想求针对每个 i，找到它左边最大值 leftMax，右边的最大值 rightMax，然后 min(leftMax，rightMax) 为能够接到水的高度。left 和 right 指针是两边往中间移动的游标指针。最傻的解题思路是针对每个下标 i，往左循环找到第一个最大值，往右循环找到第一个最大值，然后把这两个最大值取出最小者，即为当前雨水的高度。这样做时间复杂度高，浪费了很多循环。i 在从左往右的过程中，是可以动态维护最大值的。右边的最大值用右边的游标指针来维护。从左往右扫一遍下标，和，从两边往中间遍历一遍下标，是相同的结果，每个下标都遍历了一次。
  
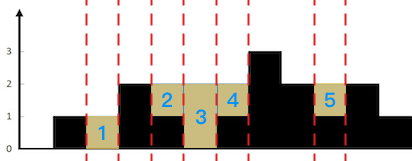
• 每个 i 的宽度固定为 1，所以每个“坑”只需要求出高度，即当前这个“坑”能积攒的雨水。最后依次将每个“坑”中的雨水相加即是能接到的雨水数。
  

代码 #

package leetcode

func trap(height []int) int {
	res, left, right, maxLeft, maxRight := 0, 0, len(height)-1, 0, 0
	for left <= right {
		if height[left] <= height[right] {
			if height[left] > maxLeft {
				maxLeft = height[left]
			} else {
				res += maxLeft - height[left]
			}
			left++
		} else {
			if height[right] >= maxRight {
				maxRight = height[right]
			} else {
				res += maxRight - height[right]
			}
			right--
		}
	}
	return res
}