218. The Skyline Problem #
题目 #
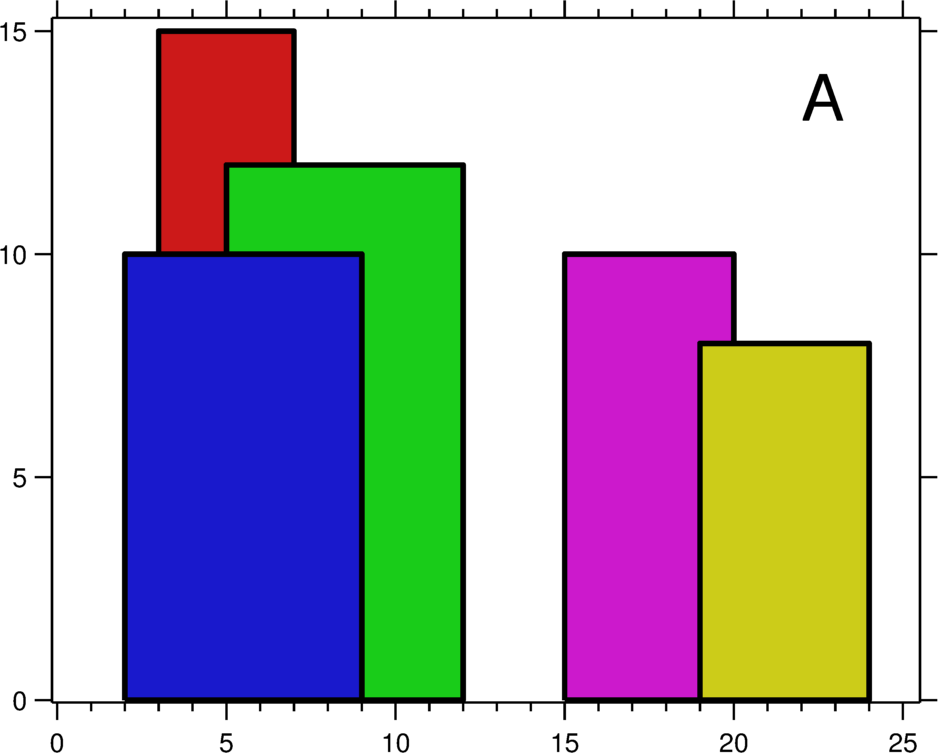
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
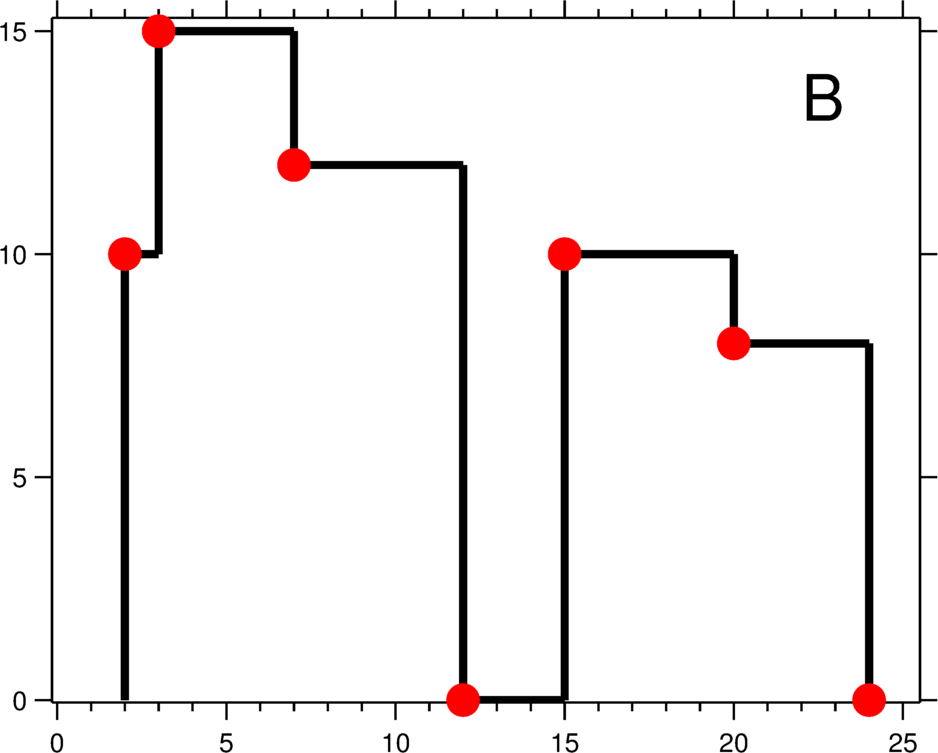
The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
- The number of buildings in any input list is guaranteed to be in the range
[0, 10000]. - The input list is already sorted in ascending order by the left x position
Li. - The output list must be sorted by the x position.
- There must be no consecutive horizontal lines of equal height in the output skyline. For instance,
[...[2 3], [4 5], [7 5], [11 5], [12 7]...]is not acceptable; the three lines of height 5 should be merged into one in the final output as such:[...[2 3], [4 5], [12 7], ...]
题目大意 #
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在,假设您获得了城市风光照片(图A)上显示的所有建筑物的位置和高度,请编写一个程序以输出由这些建筑物形成的天际线(图B)。
每个建筑物的几何信息用三元组 [Li,Ri,Hi] 表示,其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标,Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。
例如,图 A 中所有建筑物的尺寸记录为:[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。
输出是以 [ [x1,y1], [x2, y2], [x3, y3], … ] 格式的“关键点”(图 B 中的红点)的列表,它们唯一地定义了天际线。关键点是水平线段的左端点。请注意,最右侧建筑物的最后一个关键点仅用于标记天际线的终点,并始终为零高度。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
例如,图 B 中的天际线应该表示为:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。
说明:
- 任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
- 输入列表已经按左 x 坐标 Li 进行升序排列。
- 输出列表必须按 x 位排序。
- 输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[…[2 3], [4 5], [12 7], …]
解题思路 #
给出一个二维数组,每个子数组里面代表一个高楼的信息,一个高楼的信息包含 3 个信息,高楼起始坐标,高楼终止坐标,高楼高度。要求找到这些高楼的边际点,并输出这些边际点的高度信息。
这一题可以用树状数组来解答。要求天际线,即找到楼与楼重叠区间外边缘的线,说白了是维护各个区间内的最值。这有 2 个需要解决的问题。
- 如何维护最值。当一个高楼的右边界消失,剩下的各个小楼间还需要选出最大值作为天际线。剩下重重叠叠的小楼很多,树状数组如何维护区间最值是解决此类题的关键。
- 如何维护天际线的转折点。有些楼与楼并非完全重叠,重叠一半的情况导致天际线出现转折点。如上图中标记的红色转折点。树状数组如何维护这些点呢?
先解决第一个问题(维护最值)。树状数组只有 2 个操作,一个是 Add() 一个是 Query()。从上面关于这 2 个操作的讲解中可以知道这 2 个操作都不能满足我们的需求。Add() 操作可以改成维护区间内 max() 的操作。但是 max() 容易获得却很难“去除”。如上图 [3,7] 这个区间内的最大值是 15。根据树状数组的定义,[3,12] 这个区间内最值还是 15。观察上图可以看到 [5,12] 区间内最值其实是 12。树状数组如何维护这种最值呢?最大值既然难以“去除”,那么需要考虑如何让最大值“来的晚一点”。解决办法是将 Query() 操作含义从前缀含义改成后缀含义。Query(i) 查询区间是 [1,i],现在查询区间变成 \([i,+\infty)\) 。例如:[i,j] 区间内最值是 \(max_{i...j}\) ,Query(j+1) 的结果不会包含 \(max_{i...j}\) ,因为它查询的区间是 \([j+1,+\infty)\) 。这样更改以后,可以有效避免前驱高楼对后面楼的累积 max() 最值的影响。具体做法,将 x 轴上的各个区间排序,按照 x 值大小从小到大排序。从左往右依次遍历各个区间。Add() 操作含义是加入每个区间右边界代表后缀区间的最值。这样不需要考虑“移除”最值的问题了。细心的读者可能又有疑问了:能否从右往左遍历区间,Query() 的含义继续延续前缀区间?这样做是可行的,解决第一个问题(维护最值)是可以的。但是这种处理办法解决第二个问题(维护转折点)会遇到麻烦。
再解决第二个问题(维护转折点)。如果用前缀含义的 Query(),在单点 i 上除了考虑以这个点为结束点的区间,还需要考虑以这个单点 i 为起点的区间。如果是后缀含义的 Query() 就没有这个问题了, \([i+1,+\infty)\) 这个区间内不用考虑以单点 i 为结束点的区间。此题用树状数组代码实现见下面解法一。
这一题也可以用线段树来解。用线段树来解答,可以不用关心“楼挡住楼”的情况。由于楼的坐标是离散的,所以先把楼在 X 轴上两个坐标离散化。同第 699 题一样,楼的宽度是一个区间,但是离散的过程中,楼的宽度右边界需要减一,不然查询一个区间会包含两个点,导致错误的结果,例如,第一个楼是 [1,3),楼高 10,第二个楼是 [3,6),楼高 20 。第一个楼如果算上右边界 3,查询 [1,3] 的结果是 20,因为 [3,3] 这个点会查询到第二个楼上面去。所以每个楼的右边界应该减一。但是每个楼的右边界也要加入到 query 中,因为最终 query 的结果需要包含这些边界。将离散的数据排序以后,按照楼的信息,每个区间依次 update。最后统计的时候依次统计每个区间,如果当前区间的高度和前一个区间的高度一样,就算是等高的楼。当高度与前一个高度不相同的时候就算是天际线的边缘,就要添加到最后输出数组中。
类似的线段树的题目有:第 715 题,第 732 题,第 699 题。第 715 题是区间更新定值(不是增减),第 218 题可以用扫描线,第 732 题和第 699 题类似,也是俄罗斯方块的题目,但是第 732 题的俄罗斯方块的方块会“断裂”。
这一题用线段树做时间复杂度有点高,可以用扫描线解题。扫描线的思路很简单,用一根根垂直于 X 轴的竖线,从最左边依次扫到最右边,扫描每一条大楼的边界,当进入大楼的左边界的时候,如果没有比这个左边界最高点更高的点,就记录下这个最高点 keyPoint,状态是进入状态。如果扫到一个大楼的左边界,有比它更高的高度,就不记录,因为它不是天际线,它被楼挡楼,挡在其他楼后面了。当扫到一个大楼的右边界的时候,如果是最高点,那么记录下它的状态是离开状态,此时还需要记录下第二高的点。在扫描线扫描的过程中,动态的维护大楼的高度,同时维护最高的高度和第二高的高度。其实只需要维护最高的高度这一个高度,因为当离开状态到来的时候,移除掉当前最高的,剩下的高度里面最高的就是第二高的高度。描述的伪代码如下:
// 扫描线伪代码 events = {{x: L , height: H , type: entering}, {x: R , height: H , type: leaving}} event.SortByX() ds = new DS() for e in events: if entering(e): if e.height > ds.max(): ans += [e.height] ds.add(e.height) if leaving(e): ds.remove(e.height) if e.height > ds.max(): ans += [ds.max()]动态插入,查找最大值可以选用的数据结构有,最大堆和二叉搜索树。最大堆找最大值 O(1),插入 O(log n),但是 remove_by_key 需要 O(n) 的时间复杂度,并且需要自己实现。二叉搜索树,查找 max,添加和删除元素都是 O(log n) 的时间复杂度。
排序的时候也需要注意几个问题:如果大楼的边界相等,并且是进入状态,那么再按照高度从大到小进行排序;如果大楼的边界相等,并且是离开状态,那么高度按照从小到大进行排序。
代码 #
package leetcode
import (
"sort"
"github.com/halfrost/leetcode-go/template"
)
// 解法一 树状数组,时间复杂度 O(n log n)
const LEFTSIDE = 1
const RIGHTSIDE = 2
type Point struct {
xAxis int
side int
index int
}
func getSkyline(buildings [][]int) [][]int {
res := [][]int{}
if len(buildings) == 0 {
return res
}
allPoints, bit := make([]Point, 0), BinaryIndexedTree{}
// [x-axis (value), [1 (left) | 2 (right)], index (building number)]
for i, b := range buildings {
allPoints = append(allPoints, Point{xAxis: b[0], side: LEFTSIDE, index: i})
allPoints = append(allPoints, Point{xAxis: b[1], side: RIGHTSIDE, index: i})
}
sort.Slice(allPoints, func(i, j int) bool {
if allPoints[i].xAxis == allPoints[j].xAxis {
return allPoints[i].side < allPoints[j].side
}
return allPoints[i].xAxis < allPoints[j].xAxis
})
bit.Init(len(allPoints))
kth := make(map[Point]int)
for i := 0; i < len(allPoints); i++ {
kth[allPoints[i]] = i
}
for i := 0; i < len(allPoints); i++ {
pt := allPoints[i]
if pt.side == LEFTSIDE {
bit.Add(kth[Point{xAxis: buildings[pt.index][1], side: RIGHTSIDE, index: pt.index}], buildings[pt.index][2])
}
currHeight := bit.Query(kth[pt] + 1)
if len(res) == 0 || res[len(res)-1][1] != currHeight {
if len(res) > 0 && res[len(res)-1][0] == pt.xAxis {
res[len(res)-1][1] = currHeight
} else {
res = append(res, []int{pt.xAxis, currHeight})
}
}
}
return res
}
type BinaryIndexedTree struct {
tree []int
capacity int
}
// Init define
func (bit *BinaryIndexedTree) Init(capacity int) {
bit.tree, bit.capacity = make([]int, capacity+1), capacity
}
// Add define
func (bit *BinaryIndexedTree) Add(index int, val int) {
for ; index > 0; index -= index & -index {
bit.tree[index] = max(bit.tree[index], val)
}
}
// Query define
func (bit *BinaryIndexedTree) Query(index int) int {
sum := 0
for ; index <= bit.capacity; index += index & -index {
sum = max(sum, bit.tree[index])
}
return sum
}
// 解法二 线段树 Segment Tree,时间复杂度 O(n log n)
func getSkyline1(buildings [][]int) [][]int {
st, ans, lastHeight, check := template.SegmentTree{}, [][]int{}, 0, false
posMap, pos := discretization218(buildings)
tmp := make([]int, len(posMap))
st.Init(tmp, func(i, j int) int {
return max(i, j)
})
for _, b := range buildings {
st.UpdateLazy(posMap[b[0]], posMap[b[1]-1], b[2])
}
for i := 0; i < len(pos); i++ {
h := st.QueryLazy(posMap[pos[i]], posMap[pos[i]])
if check == false && h != 0 {
ans = append(ans, []int{pos[i], h})
check = true
} else if i > 0 && h != lastHeight {
ans = append(ans, []int{pos[i], h})
}
lastHeight = h
}
return ans
}
func discretization218(positions [][]int) (map[int]int, []int) {
tmpMap, posArray, posMap := map[int]int{}, []int{}, map[int]int{}
for _, pos := range positions {
tmpMap[pos[0]]++
tmpMap[pos[1]-1]++
tmpMap[pos[1]]++
}
for k := range tmpMap {
posArray = append(posArray, k)
}
sort.Ints(posArray)
for i, pos := range posArray {
posMap[pos] = i
}
return posMap, posArray
}
func max(a int, b int) int {
if a > b {
return a
}
return b
}
// 解法三 扫描线 Sweep Line,时间复杂度 O(n log n)
func getSkyline2(buildings [][]int) [][]int {
size := len(buildings)
es := make([]E, 0)
for i, b := range buildings {
l := b[0]
r := b[1]
h := b[2]
// 1-- enter
el := NewE(i, l, h, 0)
es = append(es, el)
// 0 -- leave
er := NewE(i, r, h, 1)
es = append(es, er)
}
skyline := make([][]int, 0)
sort.Slice(es, func(i, j int) bool {
if es[i].X == es[j].X {
if es[i].T == es[j].T {
if es[i].T == 0 {
return es[i].H > es[j].H
}
return es[i].H < es[j].H
}
return es[i].T < es[j].T
}
return es[i].X < es[j].X
})
pq := NewIndexMaxPQ(size)
for _, e := range es {
curH := pq.Front()
if e.T == 0 {
if e.H > curH {
skyline = append(skyline, []int{e.X, e.H})
}
pq.Enque(e.N, e.H)
} else {
pq.Remove(e.N)
h := pq.Front()
if curH > h {
skyline = append(skyline, []int{e.X, h})
}
}
}
return skyline
}
// 扫面线伪代码
// events = {{x: L , height: H , type: entering},
// {x: R , height: H , type: leaving}}
// event.SortByX()
// ds = new DS()
// for e in events:
// if entering(e):
// if e.height > ds.max(): ans += [e.height]
// ds.add(e.height)
// if leaving(e):
// ds.remove(e.height)
// if e.height > ds.max(): ans += [ds.max()]
// E define
type E struct { // 定义一个 event 事件
N int // number 编号
X int // x 坐标
H int // height 高度
T int // type 0-进入 1-离开
}
// NewE define
func NewE(n, x, h, t int) E {
return E{
N: n,
X: x,
H: h,
T: t,
}
}
// IndexMaxPQ define
type IndexMaxPQ struct {
items []int
pq []int
qp []int
total int
}
// NewIndexMaxPQ define
func NewIndexMaxPQ(n int) IndexMaxPQ {
qp := make([]int, n)
for i := 0; i < n; i++ {
qp[i] = -1
}
return IndexMaxPQ{
items: make([]int, n),
pq: make([]int, n+1),
qp: qp,
}
}
// Enque define
func (q *IndexMaxPQ) Enque(key, val int) {
q.total++
q.items[key] = val
q.pq[q.total] = key
q.qp[key] = q.total
q.swim(q.total)
}
// Front define
func (q *IndexMaxPQ) Front() int {
if q.total < 1 {
return 0
}
return q.items[q.pq[1]]
}
// Remove define
func (q *IndexMaxPQ) Remove(key int) {
rank := q.qp[key]
q.exch(rank, q.total)
q.total--
q.qp[key] = -1
q.sink(rank)
}
func (q *IndexMaxPQ) sink(n int) {
for 2*n <= q.total {
k := 2 * n
if k < q.total && q.less(k, k+1) {
k++
}
if q.less(k, n) {
break
}
q.exch(k, n)
n = k
}
}
func (q *IndexMaxPQ) swim(n int) {
for n > 1 {
k := n / 2
if q.less(n, k) {
break
}
q.exch(n, k)
n = k
}
}
func (q *IndexMaxPQ) exch(i, j int) {
q.pq[i], q.pq[j] = q.pq[j], q.pq[i]
q.qp[q.pq[i]] = i
q.qp[q.pq[j]] = j
}
func (q *IndexMaxPQ) less(i, j int) bool {
return q.items[q.pq[i]] < q.items[q.pq[j]]
}