304. Range Sum Query 2D - Immutable #

题目 #

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

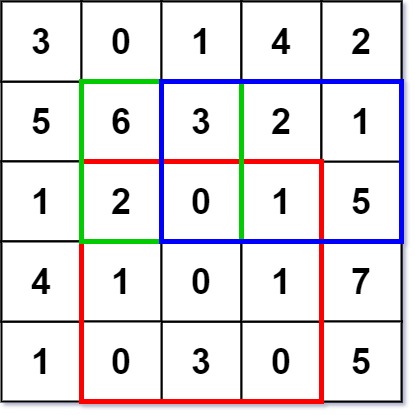
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

You may assume that the matrix does not change.
There are many calls to sumRegion function.
You may assume that row1 ≤ row2 and col1 ≤ col2.

题目大意 #

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

解题思路 #

这一题是一维数组前缀和的进阶版本。定义 f(x,y) 代表矩形左上角 (0,0)，右下角 (x,y) 内的元素和。 \[ f(i,j) = \sum_{x=0}^{i}\sum_{y=0}^{j} Matrix[x][y]\]
\[ \begin{aligned} f(i,j) &= \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j] + \sum_{y=0}^{j-1} Matrix[i][y] + Matrix[i][j]\\ &= (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{x=0}^{i-1} Matrix[x][j]) + (\sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + \sum_{y=0}^{j-1} Matrix[i][y]) - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\ &= \sum_{x=0}^{i-1}\sum_{y=0}^{j} Matrix[x][y] + \sum_{x=0}^{i}\sum_{y=0}^{j-1} Matrix[x][y] - \sum_{x=0}^{i-1}\sum_{y=0}^{j-1} Matrix[x][y] + Matrix[i][j]\\ &= f(i-1,j) + f(i,j-1) - f(i-1,j-1) + Matrix[i][j] \end{aligned} \]
于是得到递推的关系式：f(i, j) = f(i-1, j) + f(i, j-1) - f(i-1, j-1) + matrix[i][j]，写代码为了方便，新建一个 m+1 * n+1 的矩阵，这样就不需要对 row = 0 和 col = 0 做单独处理了。上述推导公式如果画成图也很好理解：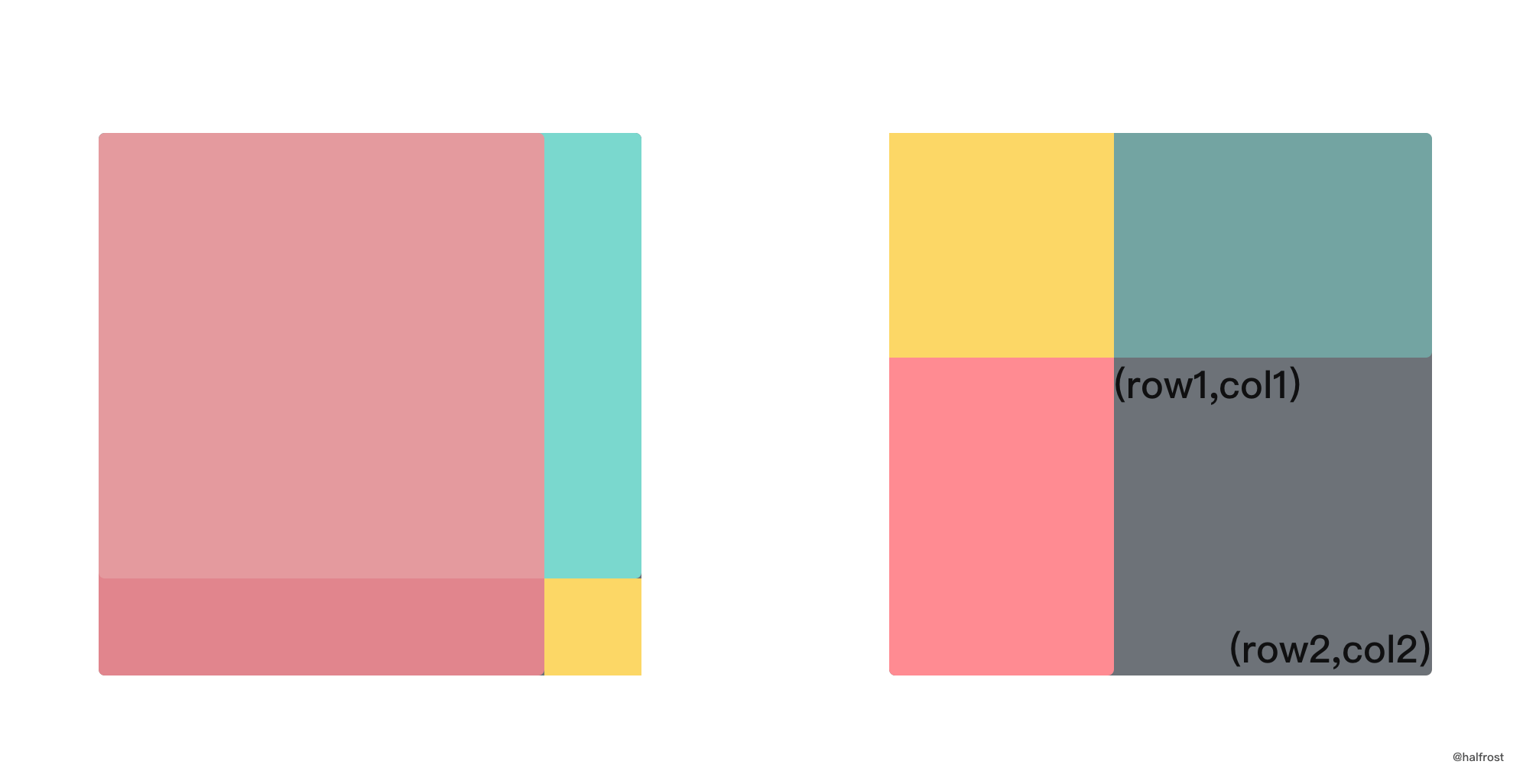
左图中大的矩形由粉红色的矩形 + 绿色矩形 - 粉红色和绿色重叠部分 + 黄色部分。这就对应的是上面推导出来的递推公式。左图是矩形左上角为 (0，0) 的情况，更加一般的情况是右图，左上角是任意的坐标，公式不变。
时间复杂度：初始化 O(mn)，查询 O(1)。空间复杂度 O(mn)

代码 #

package leetcode

type NumMatrix struct {
	cumsum [][]int
}

func Constructor(matrix [][]int) NumMatrix {
	if len(matrix) == 0 {
		return NumMatrix{nil}
	}
	cumsum := make([][]int, len(matrix)+1)
	cumsum[0] = make([]int, len(matrix[0])+1)
	for i := range matrix {
		cumsum[i+1] = make([]int, len(matrix[i])+1)
		for j := range matrix[i] {
			cumsum[i+1][j+1] = matrix[i][j] + cumsum[i][j+1] + cumsum[i+1][j] - cumsum[i][j]
		}
	}
	return NumMatrix{cumsum}
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
	cumsum := this.cumsum
	return cumsum[row2+1][col2+1] - cumsum[row1][col2+1] - cumsum[row2+1][col1] + cumsum[row1][col1]
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * obj := Constructor(matrix);
 * param_1 := obj.SumRegion(row1,col1,row2,col2);
 */

⬅️上一页

下一页➡️