419. Battleships in a Board #

题目 #

Given an m x n matrix board where each cell is a battleship 'X' or empty '.', return the number of the battleships on board.

Battleships can only be placed horizontally or vertically on board. In other words, they can only be made of the shape 1 x k (1 row, k columns) or k x 1 (k rows, 1 column), where k can be of any size. At least one horizontal or vertical cell separates between two battleships (i.e., there are no adjacent battleships).

Example 1:

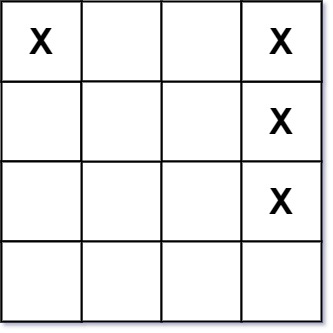
Input: board = [["X",".",".","X"],[".",".",".","X"],[".",".",".","X"]]
Output: 2

Example 2:

Input: board = [["."]]
Output: 0

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] is either '.' or 'X'.

Follow up: Could you do it in one-pass, using only O(1) extra memory and without modifying the values board?

题目大意 #

给定一个大小为m × n的矩阵 称之为甲板，矩阵单元格中的'X'表示战舰，'.'表示空位。

战舰只能水平或竖直摆放在甲板上（换句话说，可以理解为联通的同一行'X'或同一列'X'只算作一个“战舰群”），任意俩个“战舰群”间都是不相邻的。返回甲板上“战舰群”的数量。

解题思路 #

题目进阶要求一次扫描算法，空间复杂度为O(1)，且不能修改矩阵中的值。

因为题目中给定的两个“战舰群”间至少有一个水平或垂直的空位分隔，所以可以通过枚举每个战舰的左上顶点即可统计“战舰群”的个数。

假设当前遍历到矩阵中'X'的位置为(i, j)，即 board[i][j]='X'。如果当前战舰属于一个新的“战舰群”，则需要满足以下条件：

• 当前位置的上方位为空，即 board[i-1][j]='.'；
• 当前位置的左方位为空，即 board[i][j-1]='.'；

统计出所有左方位和上方位为空的战舰个数，即可得到“战舰群”的数量。