576. Out of Boundary Paths #

题目 #

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent four cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.

Example 1:

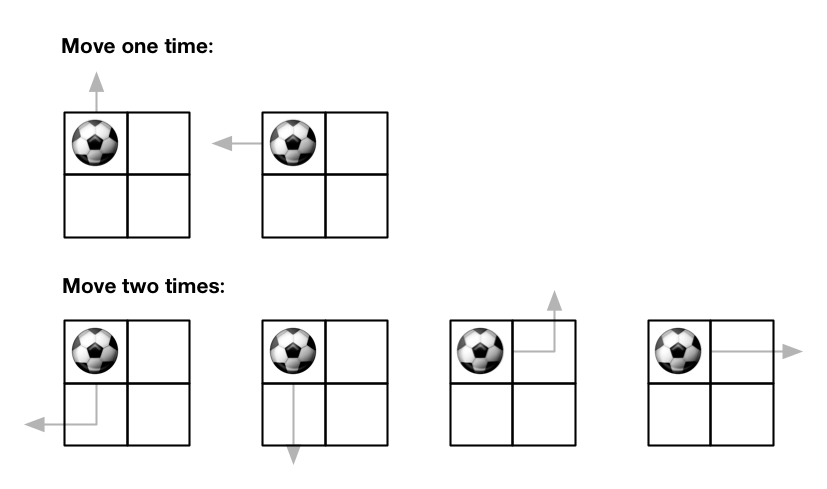
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6

Example 2:

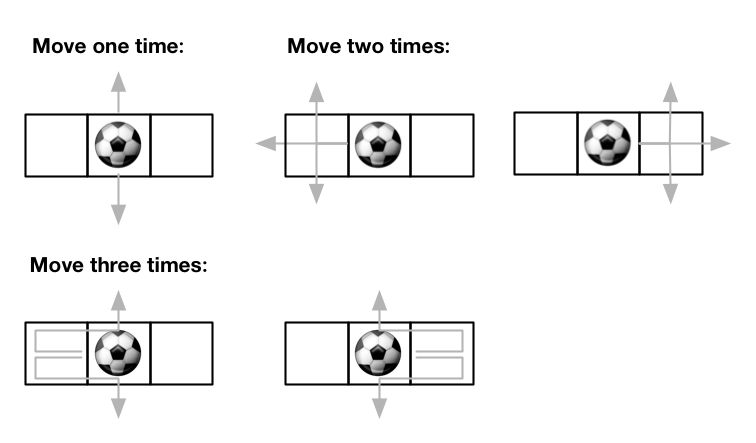
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12

Constraints:

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow <= m
• 0 <= startColumn <= n

题目大意 #

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

解题思路 #

• 单纯暴力的思路，在球的每个方向都遍历一步，直到移动步数用完。这样暴力搜索，解空间是 4^n 。优化思路便是增加记忆化。用三维数组记录位置坐标和步数，对应的出边界的路径数量。加上记忆化以后的深搜解法 runtime beats 100% 了。

代码 #

package leetcode

var dir = [][]int{
	{-1, 0},
	{0, 1},
	{1, 0},
	{0, -1},
}

func findPaths(m int, n int, maxMove int, startRow int, startColumn int) int {
	visited := make([][][]int, m)
	for i := range visited {
		visited[i] = make([][]int, n)
		for j := range visited[i] {
			visited[i][j] = make([]int, maxMove+1)
			for l := range visited[i][j] {
				visited[i][j][l] = -1
			}
		}
	}
	return dfs(startRow, startColumn, maxMove, m, n, visited)
}

func dfs(x, y, maxMove, m, n int, visited [][][]int) int {
	if x < 0 || x >= m || y < 0 || y >= n {
		return 1
	}
	if maxMove == 0 {
		visited[x][y][maxMove] = 0
		return 0
	}
	if visited[x][y][maxMove] >= 0 {
		return visited[x][y][maxMove]
	}
	res := 0
	for i := 0; i < 4; i++ {
		nx := x + dir[i][0]
		ny := y + dir[i][1]
		res += (dfs(nx, ny, maxMove-1, m, n, visited) % 1000000007)
	}
	visited[x][y][maxMove] = res % 1000000007
	return visited[x][y][maxMove]
}