710. Random Pick with Blacklist #

题目 #

Given a blacklist B containing unique integers from [0, N), write a function to return a uniform random integer from [0, N) which is NOT in B.

Optimize it such that it minimizes the call to system’s Math.random().

Note:

1 <= N <= 1000000000
0 <= B.length < min(100000, N)
[0, N) does NOT include N. See interval notation.

Example 1:


Input: 
["Solution","pick","pick","pick"]
[[1,[]],[],[],[]]
Output: [null,0,0,0]

Example 2:


Input: 
["Solution","pick","pick","pick"]
[[2,[]],[],[],[]]
Output: [null,1,1,1]

Example 3:


Input: 
["Solution","pick","pick","pick"]
[[3,[1]],[],[],[]]
Output: [null,0,0,2]

Example 4:


Input: 
["Solution","pick","pick","pick"]
[[4,[2]],[],[],[]]
Output: [null,1,3,1]

Explanation of Input Syntax:

The input is two lists: the subroutines called and their arguments. Solution’s constructor has two arguments, N and the blacklist B. pick has no arguments. Arguments are always wrapped with a list, even if there aren’t any.

题目大意 #

给一个数字 N，再给一个黑名单 B，要求在 [0,N) 区间内随机输出一个数字，这个是不在黑名单 B 中的任意一个数字。

解题思路 #

这道题的 N 的范围特别大，最大是 10 亿。如果利用桶计数，开不出来这么大的数组。考虑到题目要求我们输出的数字是随机的，所以不需要存下所有的白名单的数字。

假设 N=10, blacklist=[3, 5, 8, 9]

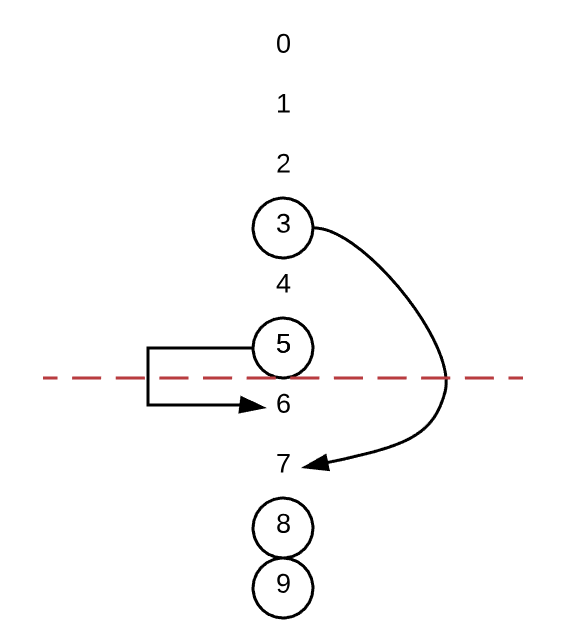
这一题有点类似 hash 冲突的意思。如果随机访问一个数，这个数正好在黑名单之内，那么就 hash 冲突了，我们就把它映射到另外一个不在黑名单里面的数中。如上图，我们可以将 3，5 重新映射到 7，6 的位置。这样末尾开始的几个数要么是黑名单里面的数，要么就是映射的数字。

hash 表总长度应该为 M = N - len(backlist)，然后在 M 的长度中扫描是否有在黑名单中的数，如果有，就代表 hash 冲突了。冲突就把这个数字映射到 (M,N) 这个区间范围内。为了提高效率，可以选择这个区间的头部或者尾部开始映射，我选择的是末尾开始映射。从 (M,N) 这个区间的末尾开始往前找，找黑名单不存在的数，找到了就把 [0,M] 区间内冲突的数字映射到这里来。最后 pick 的时候，只需要查看 map 中是否存在映射关系，如果存在就输出 map 中映射之后的值，如果没有就代表没有冲突，直接输出那个 index 即可。

代码 #


package leetcode

import "math/rand"

type Solution struct {
	M        int
	BlackMap map[int]int
}

func Constructor710(N int, blacklist []int) Solution {
	blackMap := map[int]int{}
	for i := 0; i < len(blacklist); i++ {
		blackMap[blacklist[i]] = 1
	}
	M := N - len(blacklist)
	for _, value := range blacklist {
		if value < M {
			for {
				if _, ok := blackMap[N-1]; ok {
					N--
				} else {
					break
				}
			}
			blackMap[value] = N - 1
			N--
		}
	}
	return Solution{BlackMap: blackMap, M: M}
}

func (this *Solution) Pick() int {
	idx := rand.Intn(this.M)
	if _, ok := this.BlackMap[idx]; ok {
		return this.BlackMap[idx]
	}
	return idx
}

/**
 * Your Solution object will be instantiated and called as such:
 * obj := Constructor(N, blacklist);
 * param_1 := obj.Pick();
 */

⬅️上一页

下一页➡️