952. Largest Component Size by Common Factor #

题目 #

Given a non-empty array of unique positive integers A, consider the following graph:

There are A.length nodes, labelled A[0] to A[A.length - 1];
There is an edge between A[i] and A[j] if and only if A[i]and A[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

Example 1:

Input: [4,6,15,35]
Output: 4

Example 2:

Input: [20,50,9,63]
Output: 2

Example 3:

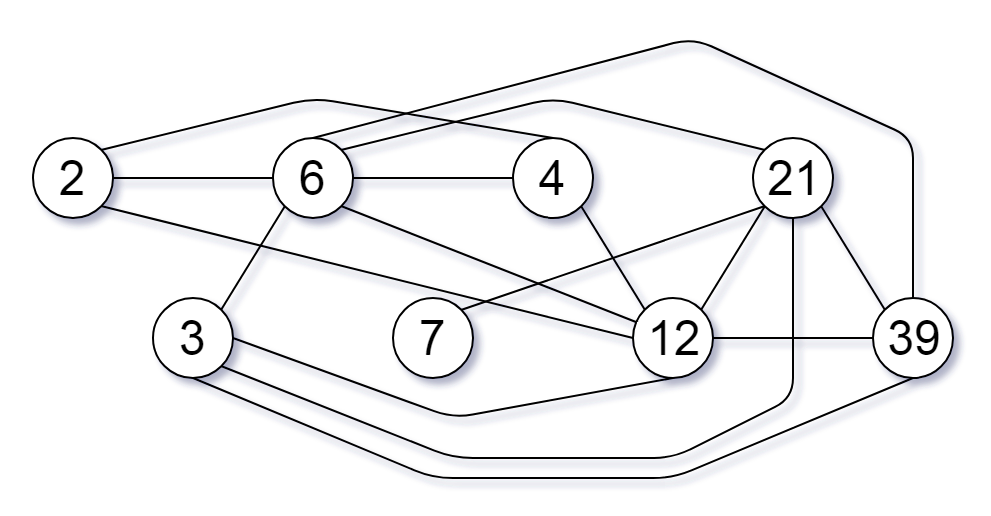
Input: [2,3,6,7,4,12,21,39]
Output: 8

Note:

1 <= A.length <= 20000
1 <= A[i] <= 100000

题目大意 #

给定一个由不同正整数的组成的非空数组 A，考虑下面的图：

有 A.length 个节点，按从 A[0] 到 A[A.length - 1] 标记；只有当 A[i] 和 A[j] 共用一个大于 1 的公因数时，A[i] 和 A[j] 之间才有一条边。返回图中最大连通组件的大小。

提示：

1 <= A.length <= 20000
1 <= A[i] <= 100000

解题思路 #

给出一个数组，数组中的元素如果每两个元素有公约数，那么这两个元素可以算有关系。所有有关系的数可以放在一个集合里，问这个数组里面有关系的元素组成的集合里面最多有多少个元素。
这一题读完题直觉就是用并查集来解题。首先可以用暴力的解法尝试。用 2 层循环，两两比较有没有公约数，如果有公约数就 union() 到一起。提交以后出现 TLE，其实看一下数据规模就知道会超时，1 <= A.length <= 20000。注意到 1 <= A[i] <= 100000，开根号以后最后才 316.66666，这个规模的数不大。所以把每个数小于根号自己的因子都找出来，例如 6 = 2 * 3，15 = 3 * 5，那么把 6 和 2，6 和 3 都 union()，15 和 3，15 和 5 都 union()，最终遍历所有的集合，找到最多元素的集合，输出它包含的元素值。

代码 #


package leetcode

import (
	"github.com/halfrost/leetcode-go/template"
)

// 解法一 并查集 UnionFind
func largestComponentSize(A []int) int {
	maxElement, uf, countMap, res := 0, template.UnionFind{}, map[int]int{}, 1
	for _, v := range A {
		maxElement = max(maxElement, v)
	}
	uf.Init(maxElement + 1)
	for _, v := range A {
		for k := 2; k*k <= v; k++ {
			if v%k == 0 {
				uf.Union(v, k)
				uf.Union(v, v/k)
			}
		}
	}
	for _, v := range A {
		countMap[uf.Find(v)]++
		res = max(res, countMap[uf.Find(v)])
	}
	return res
}

// 解法二 UnionFindCount
func largestComponentSize1(A []int) int {
	uf, factorMap := template.UnionFindCount{}, map[int]int{}
	uf.Init(len(A))
	for i, v := range A {
		for k := 2; k*k <= v; k++ {
			if v%k == 0 {
				if _, ok := factorMap[k]; !ok {
					factorMap[k] = i
				} else {
					uf.Union(i, factorMap[k])
				}
				if _, ok := factorMap[v/k]; !ok {
					factorMap[v/k] = i
				} else {
					uf.Union(i, factorMap[v/k])
				}
			}
		}
		if _, ok := factorMap[v]; !ok {
			factorMap[v] = i
		} else {
			uf.Union(i, factorMap[v])
		}
	}
	return uf.MaxUnionCount()
}

⬅️上一页

下一页➡️