968. Binary Tree Cameras #

题目 #

Given a binary tree, we install cameras on the nodes of the tree.

Each camera at a node can monitor its parent, itself, and its immediate children.

Calculate the minimum number of cameras needed to monitor all nodes of the tree.

Example 1:

Input: [0,0,null,0,0]
Output: 1
Explanation: One camera is enough to monitor all nodes if placed as shown.

Example 2:

Input: [0,0,null,0,null,0,null,null,0]
Output: 2
Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.

Note:

1. The number of nodes in the given tree will be in the range [1, 1000].
2. Every node has value 0.

题目大意 #

给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

解题思路 #

• 给出一棵树，要求在这个树上面放摄像头，一个摄像头最多可以监视 4 个节点，2 个孩子，本身节点，还有父亲节点。问最少放多少个摄像头可以覆盖树上的所有节点。
• 这一题可以用贪心思想来解题。先将节点分为 3 类，第一类，叶子节点，第二类，包含叶子节点的节点，第三类，其中一个叶子节点上放了摄像头的。按照这个想法，将树的每个节点染色，如下图。

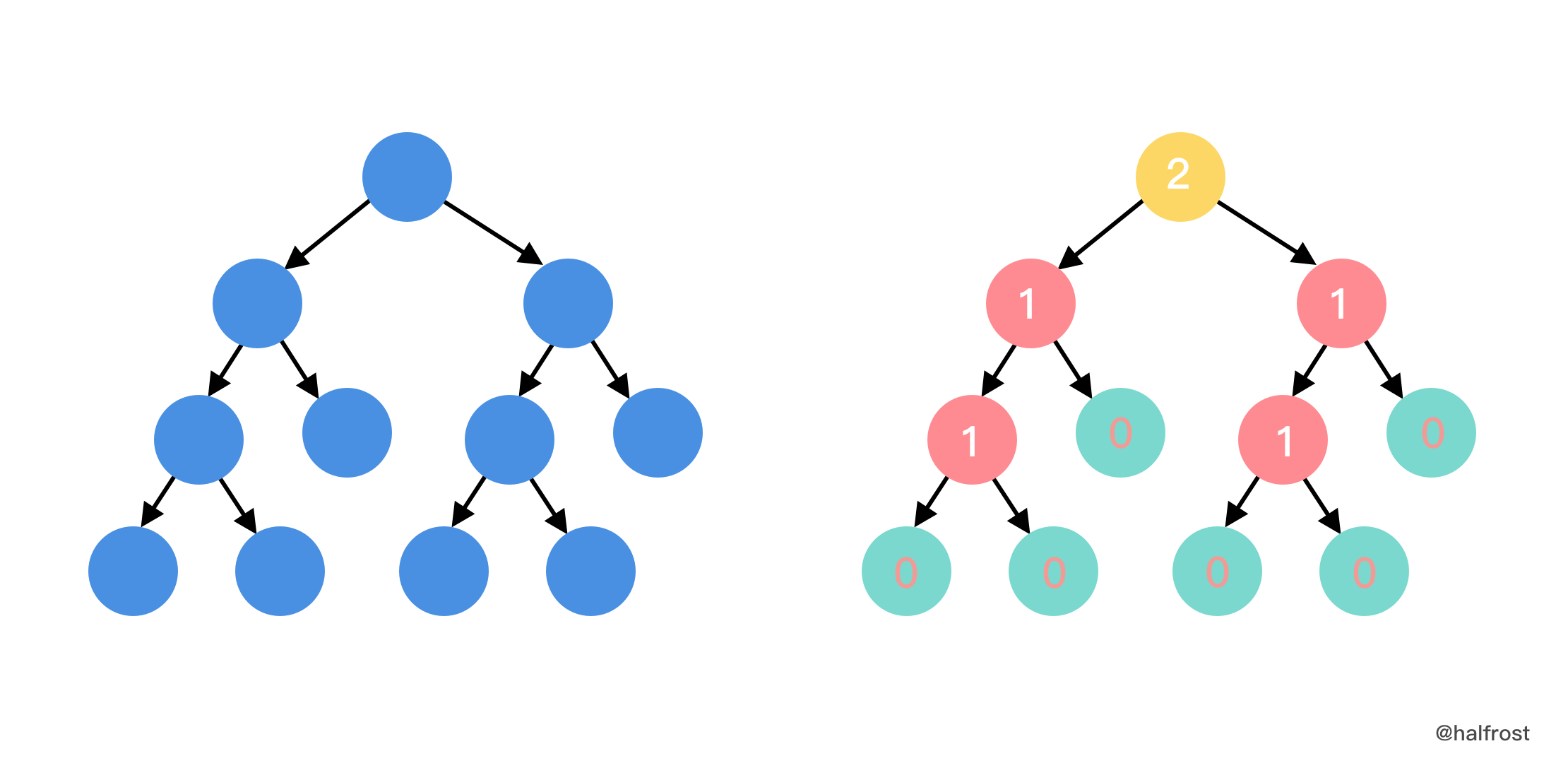
• 所有包含叶子节点的节点，可以放一个摄像头，这个可以覆盖至少 3 个节点，如果还有父节点的话，可以覆盖 4 个节点。所以贪心的策略是从最下层的叶子节点开始往上“染色”，先把最下面的一层 1 染色。标 1 的节点都是要放一个摄像头的。如果叶子节点中包含 1 的节点，那么再将这个节点染成 2 。如下图的黄色节点。黄色节点代表的是不用放摄像头的节点，因为它被叶子节点的摄像头覆盖了。出现了 2 的节点以后，再往上的节点又再次恢复成叶子节点 0 。如此类推，直到推到根节点。

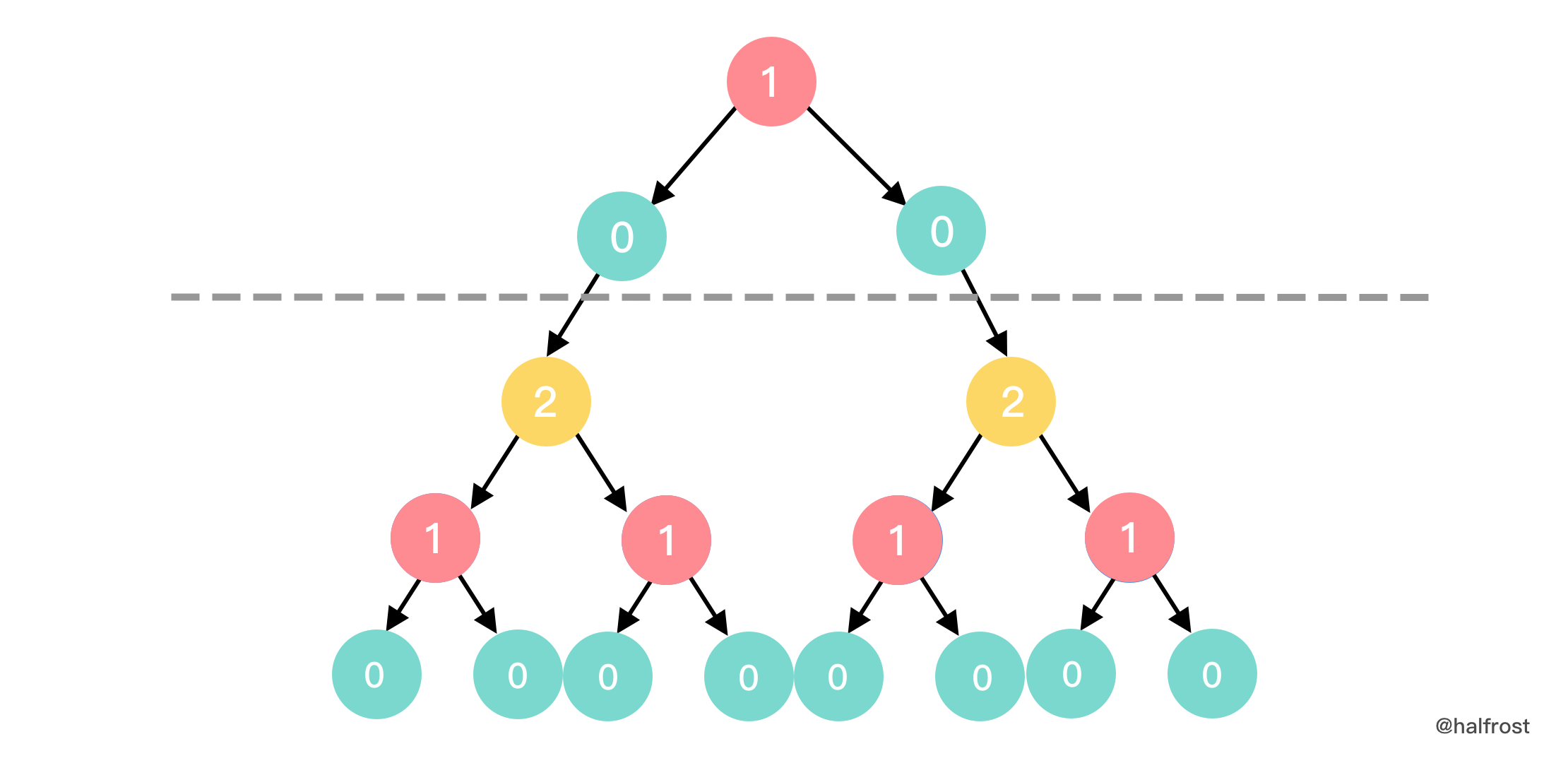
• 最后根节点还需要注意多种情况，根节点可能是叶子节点 0，那么最终答案还需要 + 1，因为需要在根节点上放一个摄像头，不然根节点覆盖不到了。根节点也有可能是 1 或者 2，这两种情况都不需要增加摄像头了，以为都覆盖到了。按照上述的方法，递归即可得到答案。

代码 #

package leetcode

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
type status int

const (
	isLeaf status = iota
	parentofLeaf
	isMonitoredWithoutCamera
)

func minCameraCover(root *TreeNode) int {
	res := 0
	if minCameraCoverDFS(root, &res) == isLeaf {
		res++
	}
	return res
}

func minCameraCoverDFS(root *TreeNode, res *int) status {
	if root == nil {
		return 2
	}
	left, right := minCameraCoverDFS(root.Left, res), minCameraCoverDFS(root.Right, res)
	if left == isLeaf || right == isLeaf {
		*res++
		return parentofLeaf
	} else if left == parentofLeaf || right == parentofLeaf {
		return isMonitoredWithoutCamera
	} else {
		return isLeaf
	}
}