979. Distribute Coins in Binary Tree #

题目 #

Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin.

Example 1:

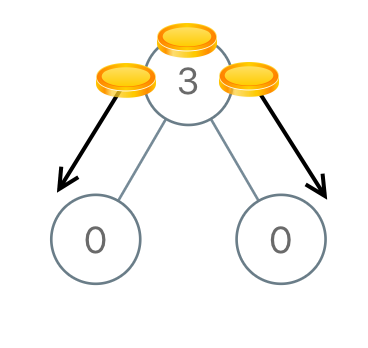
Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

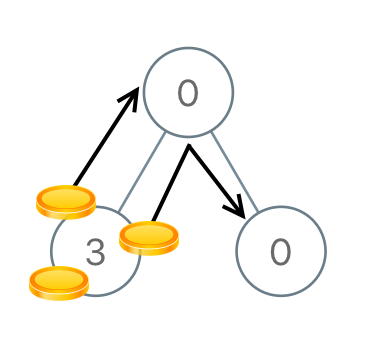
Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3:

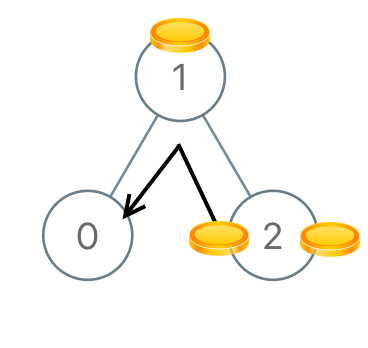
Input: [1,0,2]
Output: 2

Example 4:

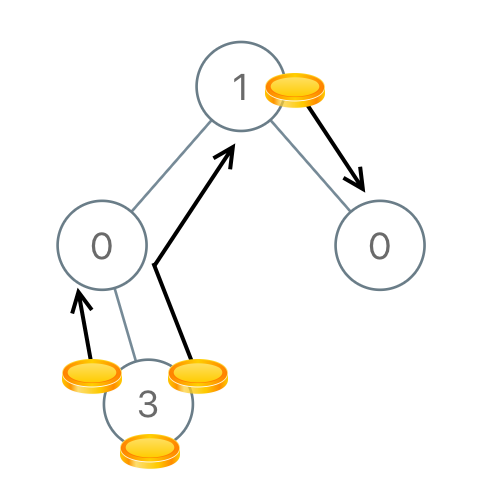
Input: [1,0,0,null,3]
Output: 4

Note:

1. 1<= N <= 100
2. 0 <= node.val <= N

题目大意 #

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点。)。返回使每个结点上只有一枚硬币所需的移动次数。

提示：

1. 1<= N <= 100
2. 0 <= node.val <= N

解题思路 #

• 给出一棵树，有 N 个节点。有 N 个硬币分散在这 N 个节点中，问经过多少次移动以后，所有节点都有一枚硬币。
• 这一题乍一看比较难分析，仔细一想，可以用贪心和分治的思想来解决。一个树的最小单元是一个根节点和两个孩子。在这种情况下，3 个节点谁的硬币多就可以分给没有硬币的那个节点，这种移动方法也能保证移动步数最少。不难证明，硬币由相邻的节点移动过来的步数是最少的。那么一棵树从最下一层开始往上推，逐步从下往上把硬币移动上去，直到最后根节点也都拥有硬币。多余 1 枚的节点记为 n -1，没有硬币的节点记为 -1 。例如，下图中左下角的 3 个节点，有 4 枚硬币的节点可以送出 3 枚硬币，叶子节点有 0 枚硬币的节点需要接收 1 枚硬币。根节点有 0 枚硬币，左孩子给了 3 枚，右孩子需要 1 枚，自己本身还要留一枚，所以最终还能剩 1 枚。

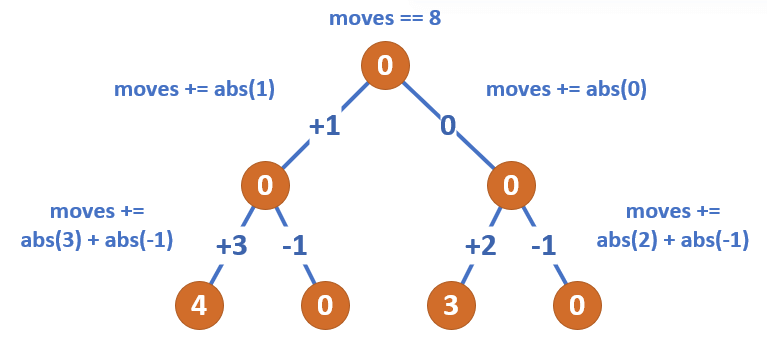
• 所以每个节点移动的步数应该是 left + right + root.Val - 1。最后递归求解即可。

代码 #

package leetcode

/**
 * Definition for a binary tree root.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func distributeCoins(root *TreeNode) int {
	res := 0
	distributeCoinsDFS(root, &res)
	return res
}

func distributeCoinsDFS(root *TreeNode, res *int) int {
	if root == nil {
		return 0
	}
	left, right := distributeCoinsDFS(root.Left, res), distributeCoinsDFS(root.Right, res)
	*res += abs(left) + abs(right)
	return left + right + root.Val - 1
}