1079. Letter Tile Possibilities #

题目 #

You have a set of tiles, where each tile has one letter tiles[i] printed on it. Return the number of possible non-empty sequences of letters you can make.

Example 1:

Input: "AAB"
Output: 8
Explanation: The possible sequences are "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA".

Example 2:

Input: "AAABBC"
Output: 188

Note:

1 <= tiles.length <= 7
tiles consists of uppercase English letters.

题目大意 #

你有一套活字字模 tiles，其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。提示：

1 <= tiles.length <= 7
tiles 由大写英文字母组成

解题思路 #

题目要求输出所有非空字母序列的数目。这一题是排列和组合的结合题目。组合是可以选择一个字母，二个字母，…… n 个字母。每个组合内是排列问题。比如选择 2 个字母，字母之间相互排序不同是影响最终结果的，不同的排列顺序是不同的解。
这道题目由于不需要输出所有解，所以解法可以优化，例如我们在递归计算解的时候，不需要真的遍历原字符串，只需要累加一些字母的频次就可以。当然如果要输出所有解，就需要真实遍历原字符串了(见解法二)。简单的做法是每次递归按照频次累加。因为每次增加一个字母一定是 26 个大写字母中的一个。这里需要注意的是，增加的只能是 26 个字母里面还能取出“机会”的字母，例如递归到到第 3 轮了，A 用完了，这个时候只能取频次还不为 0 的字母拼上去。

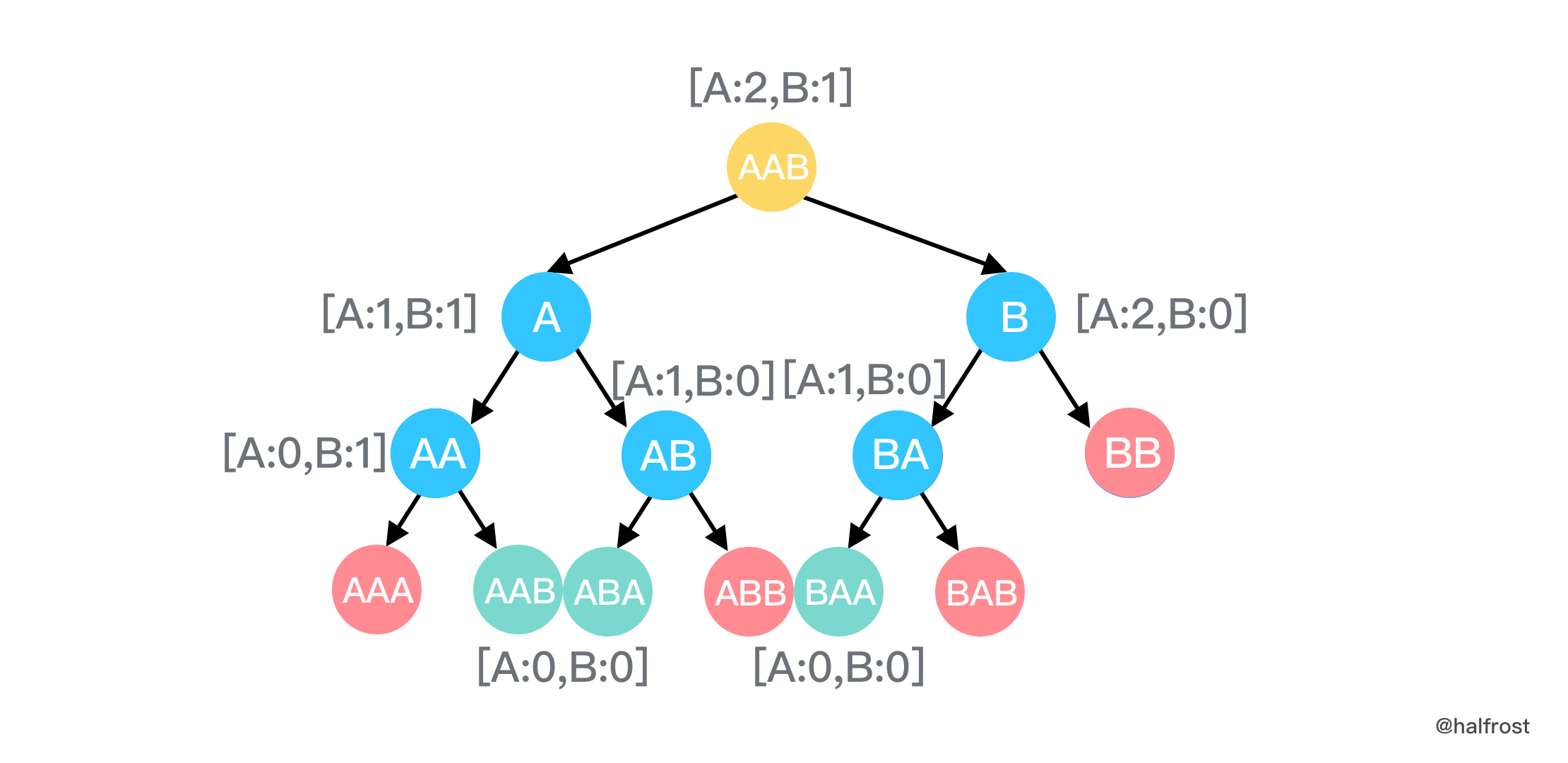
代码 #


package leetcode

// 解法一 DFS
func numTilePossibilities(tiles string) int {
	m := make(map[byte]int)
	for i := range tiles {
		m[tiles[i]]++
	}
	arr := make([]int, 0)
	for _, v := range m {
		arr = append(arr, v)
	}
	return numTileDFS(arr)
}

func numTileDFS(arr []int) (r int) {
	for i := 0; i < len(arr); i++ {
		if arr[i] == 0 {
			continue
		}
		r++
		arr[i]--
		r += numTileDFS(arr)
		arr[i]++
	}
	return
}

// 解法二 DFS 暴力解法
func numTilePossibilities1(tiles string) int {
	res, tmp, tMap, used := 0, []byte{}, make(map[string]string, 0), make([]bool, len(tiles))
	findTile([]byte(tiles), tmp, &used, 0, &res, tMap)
	return res
}

func findTile(tiles, tmp []byte, used *[]bool, index int, res *int, tMap map[string]string) {
	flag := true
	for _, v := range *used {
		if v == false {
			flag = false
			break
		}
	}
	if flag {
		return
	}
	for i := 0; i < len(tiles); i++ {
		if (*used)[i] == true {
			continue
		}
		tmp = append(tmp, tiles[i])
		(*used)[i] = true
		if _, ok := tMap[string(tmp)]; !ok {
			//fmt.Printf("i = %v tiles = %v 找到了结果 = %v\n", i, string(tiles), string(tmp))
			*res++
		}
		tMap[string(tmp)] = string(tmp)

		findTile([]byte(tiles), tmp, used, i+1, res, tMap)
		tmp = tmp[:len(tmp)-1]
		(*used)[i] = false
	}
}

⬅️上一页

下一页➡️