1091. Shortest Path in Binary Matrix #

题目 #

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
C_1 is at location (0, 0) (ie. has value grid[0][0])
C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

Example 1:

Input: [[0,1],[1,0]]
Output: 2

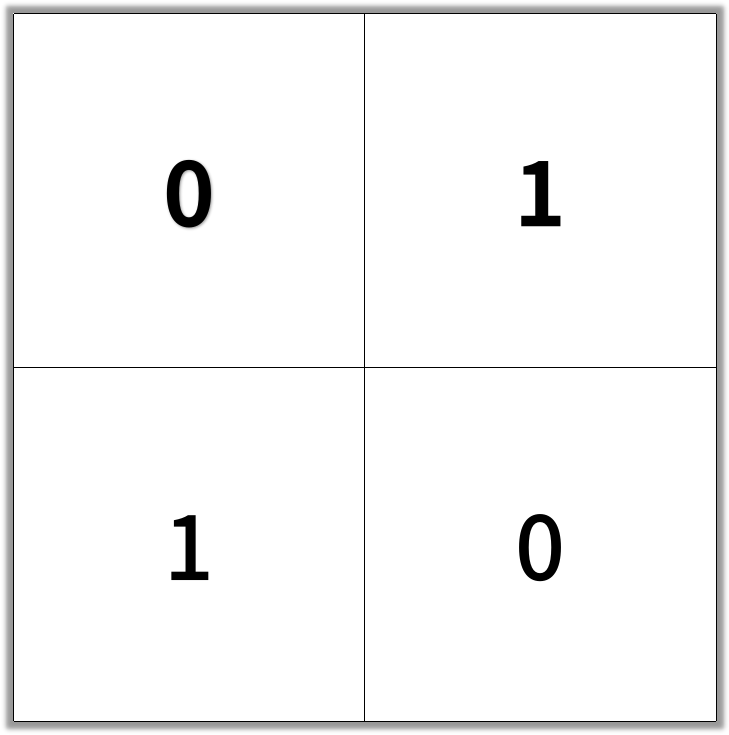
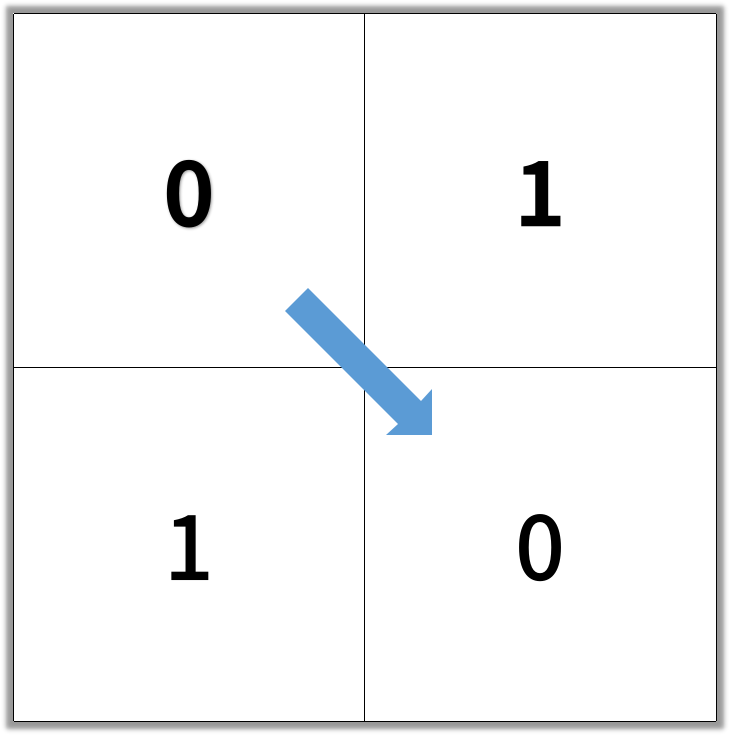
Example 2:

Input: [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

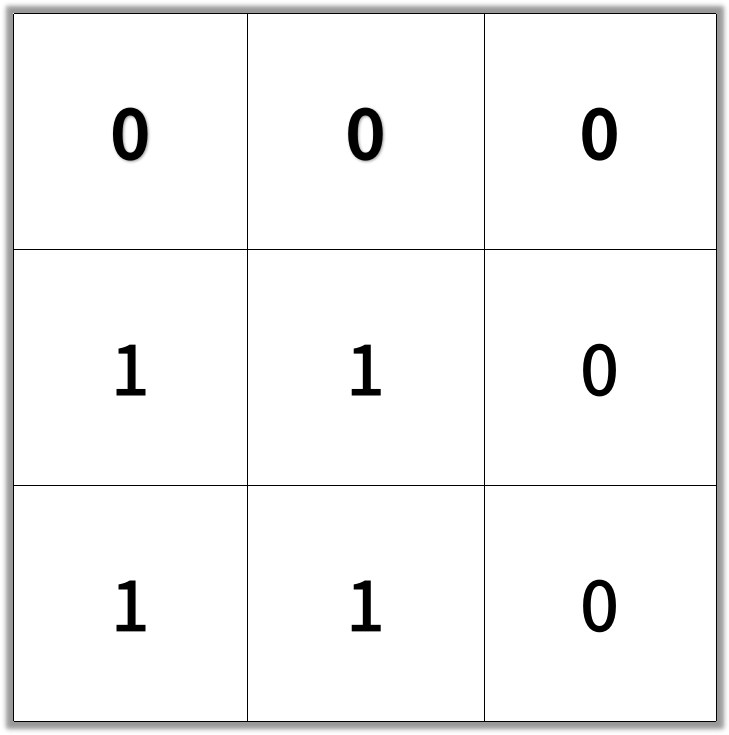
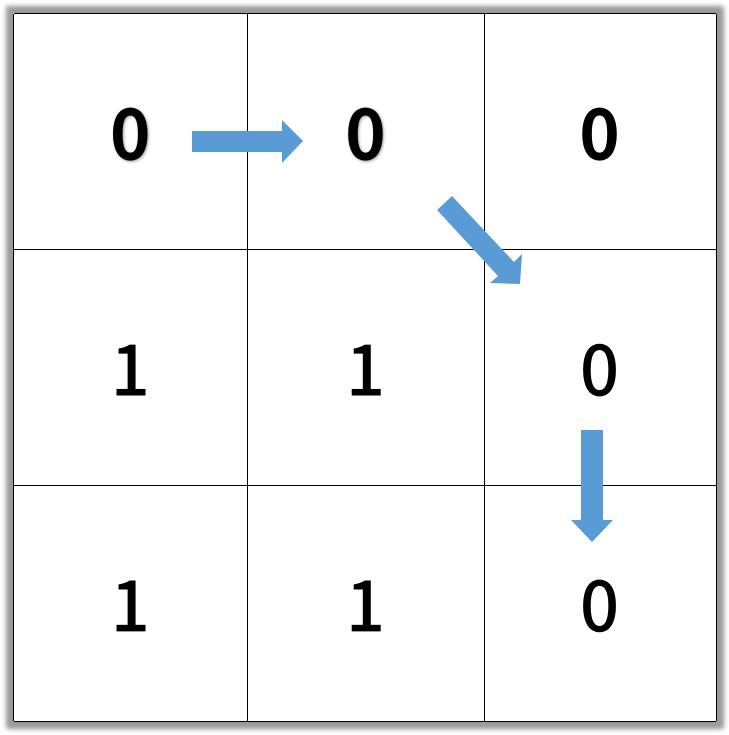
Note:

1 <= grid.length == grid[0].length <= 100
grid[r][c] is 0 or 1

题目大意 #

在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, …, C_k 组成：

相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）
C_1 位于 (0, 0)（即，值为 grid[0][0]）
C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）
如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）

返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径，返回 -1 。

解题思路 #

这一题是简单的找最短路径。利用 BFS 从左上角逐步扩展到右下角，便可以很容易求解。注意每轮扩展需要考虑 8 个方向。

代码 #

var dir = [][]int{
	{-1, -1},
	{-1, 0},
	{-1, 1},
	{0, 1},
	{0, -1},
	{1, -1},
	{1, 0},
	{1, 1},
}

func shortestPathBinaryMatrix(grid [][]int) int {
	visited := make([][]bool, 0)
	for range make([]int, len(grid)) {
		visited = append(visited, make([]bool, len(grid[0])))
	}
	dis := make([][]int, 0)
	for range make([]int, len(grid)) {
		dis = append(dis, make([]int, len(grid[0])))
	}
	if grid[0][0] == 1 {
		return -1
	}
	if len(grid) == 1 && len(grid[0]) == 1 {
		return 1
	}

	queue := []int{0}
	visited[0][0], dis[0][0] = true, 1
	for len(queue) > 0 {
		cur := queue[0]
		queue = queue[1:]
		curx, cury := cur/len(grid[0]), cur%len(grid[0])
		for d := 0; d < 8; d++ {
			nextx := curx + dir[d][0]
			nexty := cury + dir[d][1]
			if isInBoard(grid, nextx, nexty) && !visited[nextx][nexty] && grid[nextx][nexty] == 0 {
				queue = append(queue, nextx*len(grid[0])+nexty)
				visited[nextx][nexty] = true
				dis[nextx][nexty] = dis[curx][cury] + 1
				if nextx == len(grid)-1 && nexty == len(grid[0])-1 {
					return dis[nextx][nexty]
				}
			}
		}
	}
	return -1
}

func isInBoard(board [][]int, x, y int) bool {
	return x >= 0 && x < len(board) && y >= 0 && y < len(board[0])
}

⬅️上一页

下一页➡️