1203. Sort Items by Groups Respecting Dependencies #
题目 #
There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it’s equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
- The items that belong to the same group are next to each other in the sorted list.
- There are some relations between these items where
beforeItems[i]is a list containing all the items that should come before theith item in the sorted array (to the left of theith item).
Return any solution if there is more than one solution and return an empty list if there is no solution.
Example 1:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]
Example 2:
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
Constraints:
1 <= m <= n <= 3 * 104group.length == beforeItems.length == n1 <= group[i] <= m - 10 <= beforeItems[i].length <= n - 10 <= beforeItems[i][j] <= n - 1i != beforeItems[i][j]beforeItems[i]does not contain duplicates elements.
题目大意 #
有 n 个项目,每个项目或者不属于任何小组,或者属于 m 个小组之一。group[i] 表示第 i 个小组所属的小组,如果第 i 个项目不属于任何小组,则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目,即没有任何项目属于这个小组。
请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表:
- 同一小组的项目,排序后在列表中彼此相邻。
- 项目之间存在一定的依赖关系,我们用一个列表 beforeItems 来表示,其中 beforeItems[i] 表示在进行第 i 个项目前(位于第 i 个项目左侧)应该完成的所有项目。
如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。
解题思路 #
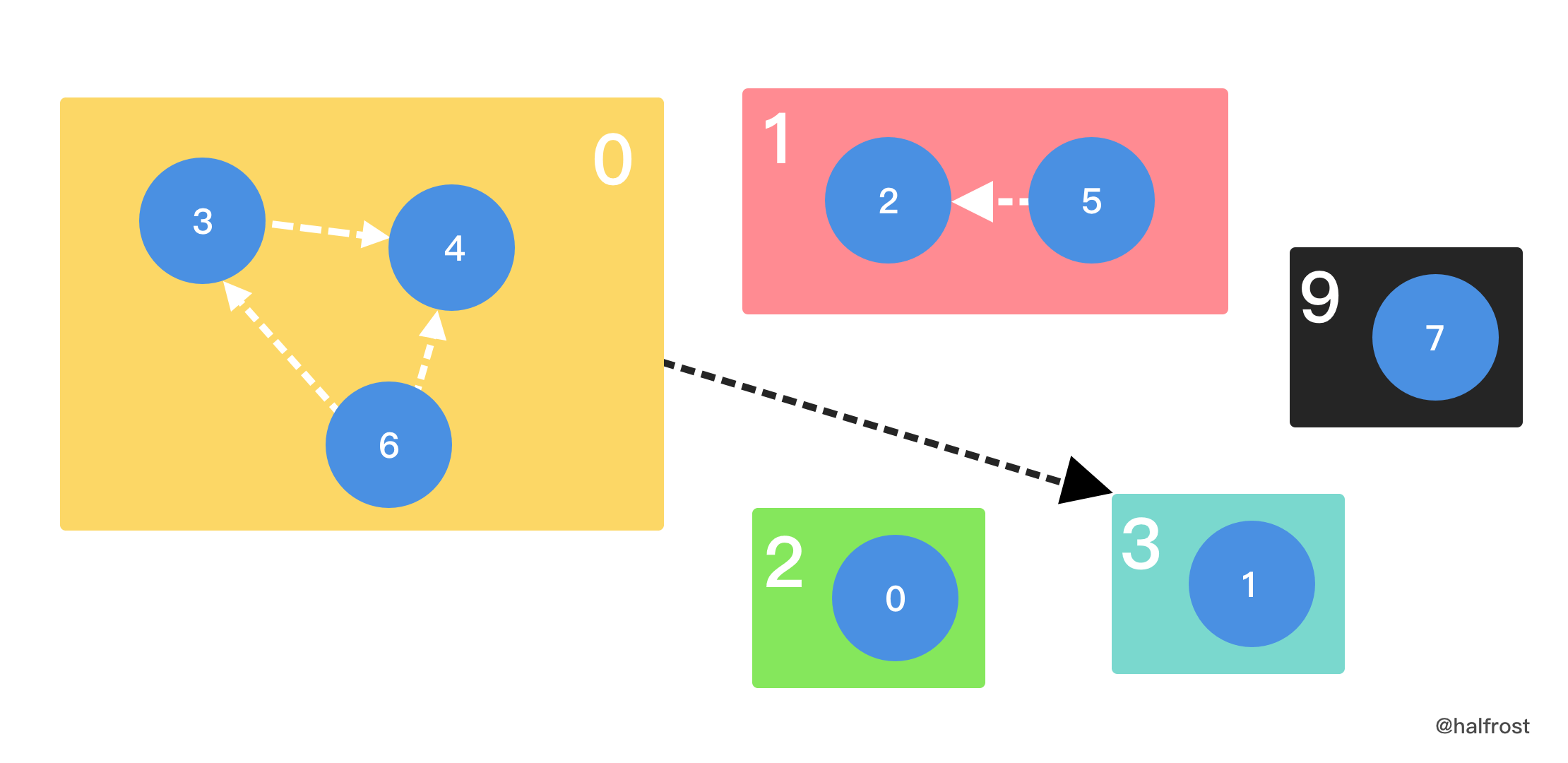
读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是,同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序,第二次拓扑排序排出组内的顺序。为了实现方便,用 map 给虚拟分组标记编号。如下图,将 3,4,6 三个任务打包到 0 号分组里面,将 2,5 两个任务打包到 1 号分组里面,其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里,所以 3 号分组依赖 0 号分组。先组间排序,确定分组顺序,再组内拓扑排序,排出最终顺序。
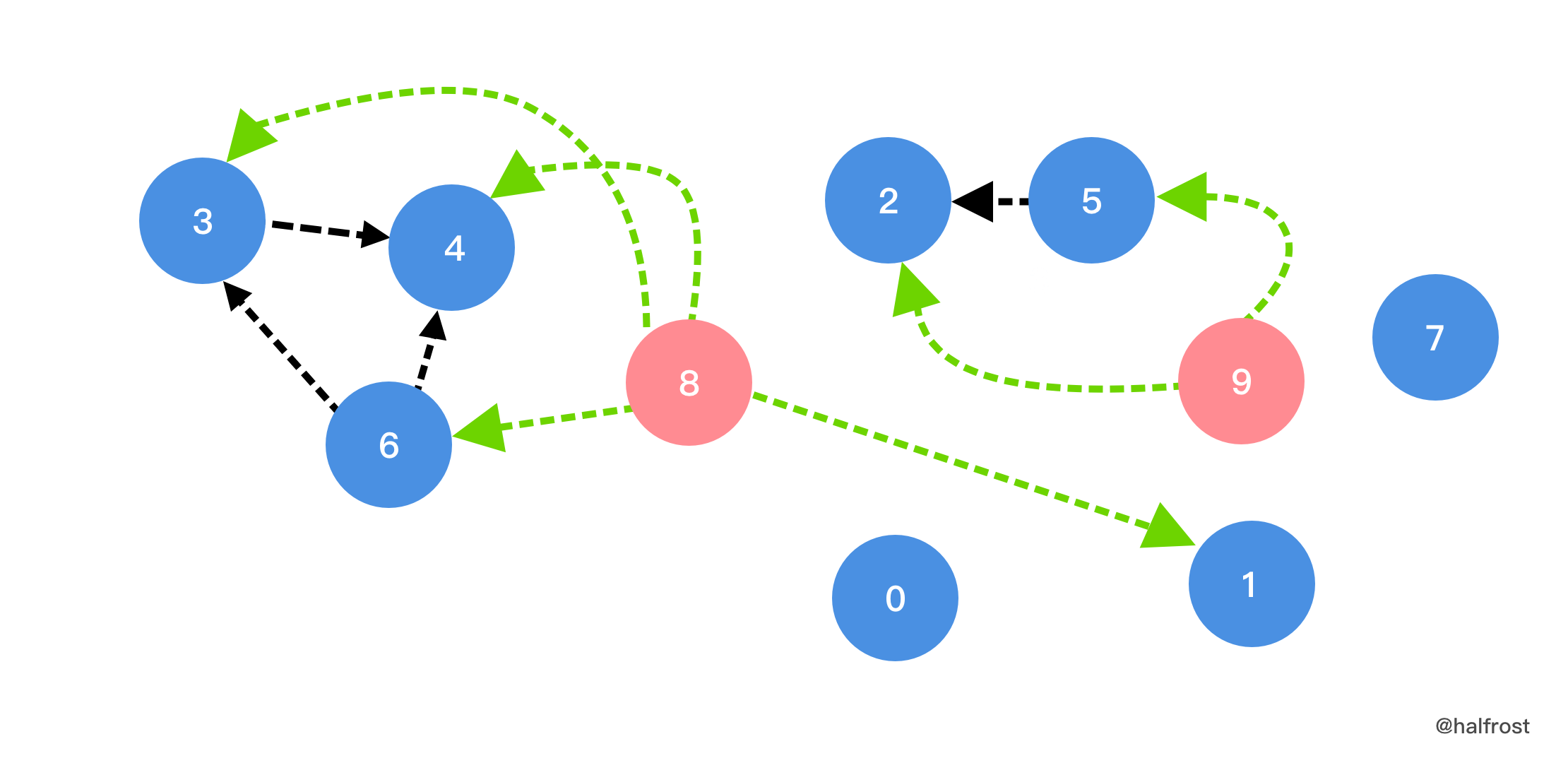
上面的解法可以 AC,但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢?将必须要在一起的结点统一依赖一个虚拟结点,例如下图中的虚拟结点 8 和 9 。3,4,6 都依赖 8 号任务,2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务,由于 6 由依赖 8 ,所以添加 1 依赖 8 的边。通过增加虚拟结点,增加了需要打包在一起结点的入度。构建出以上关系以后,按照入度为 0 的原则,依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ,对它们进行 DFS,必定会使得与它关联的节点都被安排在一起,这样就满足了题意:同一小组的项目,排序后在列表中彼此相邻。一遍扫完,满足题意的顺序就排出来了。这个解法 beat 100%!
代码 #
package leetcode
// 解法一 拓扑排序版的 DFS
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
groups, inDegrees := make([][]int, n+m), make([]int, n+m)
for i, g := range group {
if g > -1 {
g += n
groups[g] = append(groups[g], i)
inDegrees[i]++
}
}
for i, ancestors := range beforeItems {
gi := group[i]
if gi == -1 {
gi = i
} else {
gi += n
}
for _, ancestor := range ancestors {
ga := group[ancestor]
if ga == -1 {
ga = ancestor
} else {
ga += n
}
if gi == ga {
groups[ancestor] = append(groups[ancestor], i)
inDegrees[i]++
} else {
groups[ga] = append(groups[ga], gi)
inDegrees[gi]++
}
}
}
res := []int{}
for i, d := range inDegrees {
if d == 0 {
sortItemsDFS(i, n, &res, &inDegrees, &groups)
}
}
if len(res) != n {
return nil
}
return res
}
func sortItemsDFS(i, n int, res, inDegrees *[]int, groups *[][]int) {
if i < n {
*res = append(*res, i)
}
(*inDegrees)[i] = -1
for _, ch := range (*groups)[i] {
if (*inDegrees)[ch]--; (*inDegrees)[ch] == 0 {
sortItemsDFS(ch, n, res, inDegrees, groups)
}
}
}
// 解法二 二维拓扑排序 时间复杂度 O(m+n),空间复杂度 O(m+n)
func sortItems1(n int, m int, group []int, beforeItems [][]int) []int {
groupItems, res := map[int][]int{}, []int{}
for i := 0; i < len(group); i++ {
if group[i] == -1 {
group[i] = m + i
}
groupItems[group[i]] = append(groupItems[group[i]], i)
}
groupGraph, groupDegree, itemGraph, itemDegree := make([][]int, m+n), make([]int, m+n), make([][]int, n), make([]int, n)
for i := 0; i < len(beforeItems); i++ {
for j := 0; j < len(beforeItems[i]); j++ {
if group[beforeItems[i][j]] != group[i] {
// 不同组项目,确定组间依赖关系
groupGraph[group[beforeItems[i][j]]] = append(groupGraph[group[beforeItems[i][j]]], group[i])
groupDegree[group[i]]++
} else {
// 同组项目,确定组内依赖关系
itemGraph[beforeItems[i][j]] = append(itemGraph[beforeItems[i][j]], i)
itemDegree[i]++
}
}
}
items := []int{}
for i := 0; i < m+n; i++ {
items = append(items, i)
}
// 组间拓扑
groupOrders := topSort(groupGraph, groupDegree, items)
if len(groupOrders) < len(items) {
return nil
}
for i := 0; i < len(groupOrders); i++ {
items := groupItems[groupOrders[i]]
// 组内拓扑
orders := topSort(itemGraph, itemDegree, items)
if len(orders) < len(items) {
return nil
}
res = append(res, orders...)
}
return res
}
func topSort(graph [][]int, deg, items []int) (orders []int) {
q := []int{}
for _, i := range items {
if deg[i] == 0 {
q = append(q, i)
}
}
for len(q) > 0 {
from := q[0]
q = q[1:]
orders = append(orders, from)
for _, to := range graph[from] {
deg[to]--
if deg[to] == 0 {
q = append(q, to)
}
}
}
return
}