1260. Shift 2D Grid #

题目 #

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

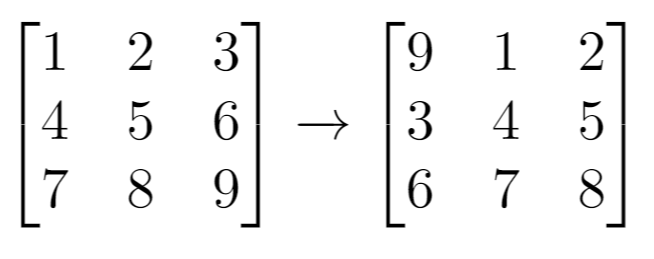
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

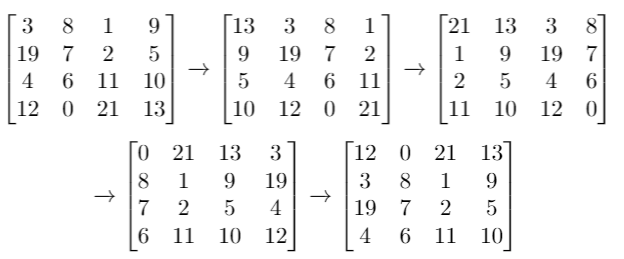
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

题目大意 #

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。每次「迁移」操作将会引发下述活动：

• 位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
• 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
• 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

解题思路 #

• 给一个矩阵和一个移动步数 k，要求把矩阵每个元素往后移动 k 步，最后的元素移动头部，循环移动，最后输出移动结束的矩阵。
• 简单题，按照题意循环移动即可，注意判断边界情况。

代码 #

package leetcode

func shiftGrid(grid [][]int, k int) [][]int {
	x, y := len(grid[0]), len(grid)
	newGrid := make([][]int, y)
	for i := 0; i < y; i++ {
		newGrid[i] = make([]int, x)
	}
	for i := 0; i < y; i++ {
		for j := 0; j < x; j++ {
			ny := (k / x) + i
			if (j + (k % x)) >= x {
				ny++
			}
			newGrid[ny%y][(j+(k%x))%x] = grid[i][j]
		}
	}
	return newGrid
}