1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts #

题目 #

Given a rectangular cake with height h and width w, and two arrays of integers horizontalCuts and verticalCuts where horizontalCuts[i] is the distance from the top of the rectangular cake to the ith horizontal cut and similarly, verticalCuts[j] is the distance from the left of the rectangular cake to the jth vertical cut.

Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a huge number, return this modulo 10^9 + 7.

Example 1:

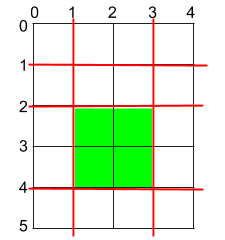
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
Output: 4
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.

Example 2:

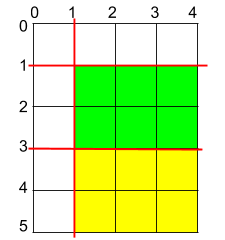
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
Output: 6
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.

Example 3:

Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
Output: 9

Constraints:

• 2 <= h, w <= 10^9
• 1 <= horizontalCuts.length < min(h, 10^5)
• 1 <= verticalCuts.length < min(w, 10^5)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• It is guaranteed that all elements in horizontalCuts are distinct.
• It is guaranteed that all elements in verticalCuts are distinct.

题目大意 #

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中 horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离，类似地， verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7 取余后返回。

解题思路 #

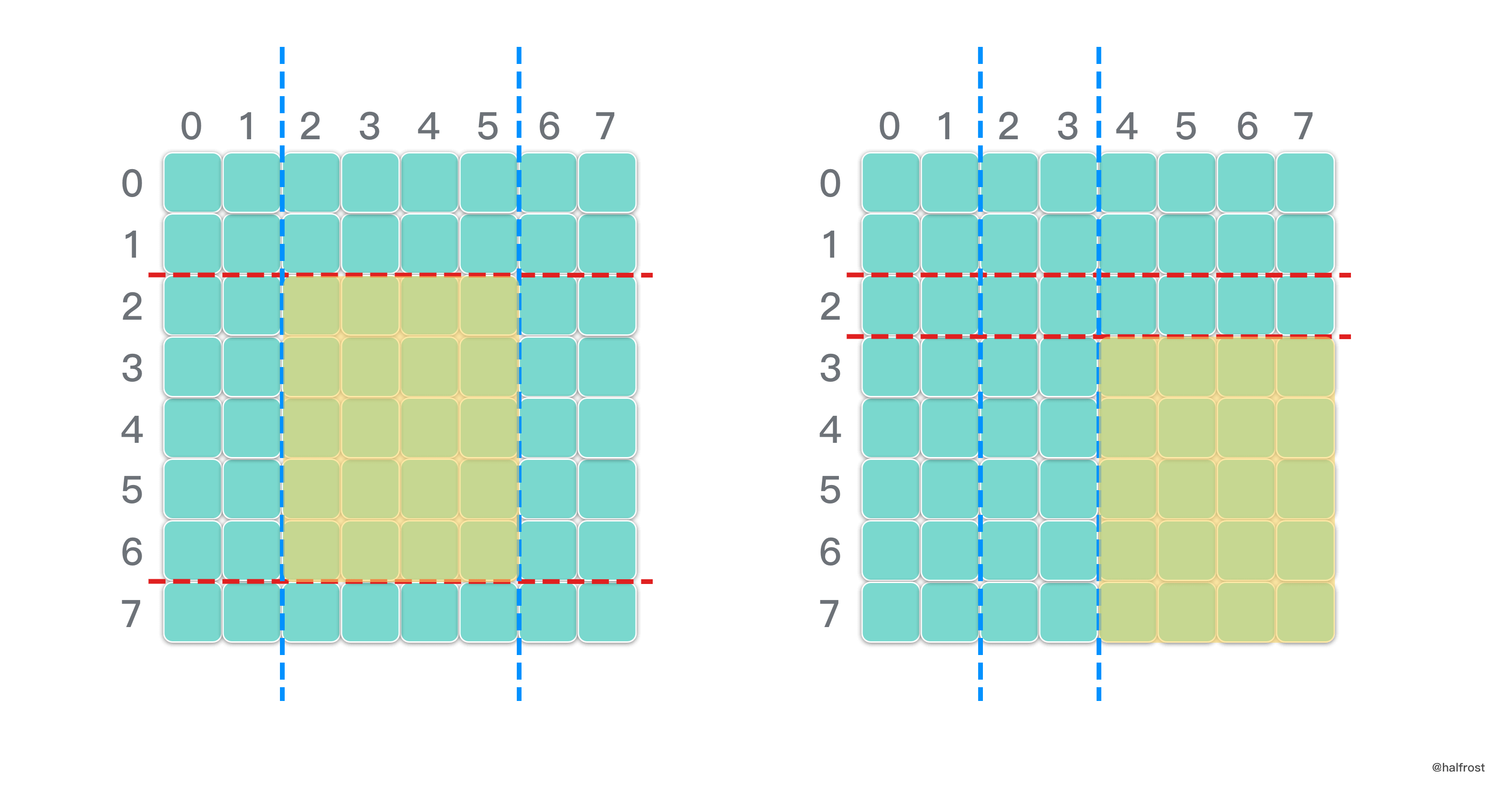
• 读完题比较容易想到解题思路。找到水平切口最大的差值和竖直切口最大的差值，这 4 条边构成的矩形即为最大矩形。不过有特殊情况需要判断，切口除了题目给的切口坐标以外，默认还有 4 个切口，即蛋糕原始的 4 条边。如下图二，最大的矩形其实在切口之外。所以找水平切口最大差值和竖直切口最大差值需要考虑到蛋糕原始的 4 条边。

代码 #

package leetcode

import "sort"

func maxArea(h int, w int, hcuts []int, vcuts []int) int {
	sort.Ints(hcuts)
	sort.Ints(vcuts)
	maxw, maxl := hcuts[0], vcuts[0]
	for i, c := range hcuts[1:] {
		if c-hcuts[i] > maxw {
			maxw = c - hcuts[i]
		}
	}
	if h-hcuts[len(hcuts)-1] > maxw {
		maxw = h - hcuts[len(hcuts)-1]
	}
	for i, c := range vcuts[1:] {
		if c-vcuts[i] > maxl {
			maxl = c - vcuts[i]
		}
	}
	if w-vcuts[len(vcuts)-1] > maxl {
		maxl = w - vcuts[len(vcuts)-1]
	}
	return (maxw * maxl) % (1000000007)
}