1648. Sell Diminishing-Valued Colored Balls #

题目 #

You have an inventory of different colored balls, and there is a customer that wants orders balls of any color.

The customer weirdly values the colored balls. Each colored ball’s value is the number of balls of that color you currently have in your inventory. For example, if you own 6 yellow balls, the customer would pay 6 for the first yellow ball. After the transaction, there are only 5 yellow balls left, so the next yellow ball is then valued at 5 (i.e., the value of the balls decreases as you sell more to the customer).

You are given an integer array, inventory, where inventory[i] represents the number of balls of the ith color that you initially own. You are also given an integer orders, which represents the total number of balls that the customer wants. You can sell the balls in any order.

Return the maximum total value that you can attain after selling orders colored balls. As the answer may be too large, return it modulo 109 + 7.

Example 1:

Input: inventory = [2,5], orders = 4
Output: 14
Explanation: Sell the 1st color 1 time (2) and the 2nd color 3 times (5 + 4 + 3).
The maximum total value is 2 + 5 + 4 + 3 = 14.

Example 2:

Input: inventory = [3,5], orders = 6
Output: 19
Explanation: Sell the 1st color 2 times (3 + 2) and the 2nd color 4 times (5 + 4 + 3 + 2).
The maximum total value is 3 + 2 + 5 + 4 + 3 + 2 = 19.

Example 3:

Input: inventory = [2,8,4,10,6], orders = 20
Output: 110

Example 4:

Input: inventory = [1000000000], orders = 1000000000
Output: 21
Explanation: Sell the 1st color 1000000000 times for a total value of 500000000500000000. 500000000500000000 modulo 109 + 7 = 21.

Constraints:

• 1 <= inventory.length <= 10^5
• 1 <= inventory[i] <= 10^9
• 1 <= orders <= min(sum(inventory[i]), 10^9)

题目大意 #

你有一些球的库存 inventory ，里面包含着不同颜色的球。一个顾客想要 任意颜色 总数为 orders 的球。这位顾客有一种特殊的方式衡量球的价值：每个球的价值是目前剩下的 同色球 的数目。比方说还剩下 6 个黄球，那么顾客买第一个黄球的时候该黄球的价值为 6 。这笔交易以后，只剩下 5 个黄球了，所以下一个黄球的价值为 5 （也就是球的价值随着顾客购买同色球是递减的）

给你整数数组 inventory ，其中 inventory[i] 表示第 i 种颜色球一开始的数目。同时给你整数 orders ，表示顾客总共想买的球数目。你可以按照 任意顺序 卖球。请你返回卖了 orders 个球以后 最大 总价值之和。由于答案可能会很大，请你返回答案对 109 + 7 取余数 的结果。

提示：

• 1 <= inventory.length <= 10^5
• 1 <= inventory[i] <= 10^9
• 1 <= orders <= min(sum(inventory[i]), 10^9)

解题思路 #

• 给出一个 inventory 数组和 orders 次操作，要求输出数组中前 orders 大个元素累加和。需要注意的是，每累加一个元素 inventory[i]，这个元素都会减一，下次再累加的时候，需要选取更新以后的数组的最大值。

• 拿到这个题目以后很容易想到优先队列，建立大根堆以后，pop 出当前最大值 maxItem，累加，以后把 maxItem 减一再 push 回去。循环执行 orders 次以后即是最终结果。题目是这个意思，但是我们不能这么写代码，因为题目条件里面给出了 orders 的数据大小。orders 最大为 10^9。按照优先队列的这个方法一定会超时，时间复杂度为 O(orders⋅logn)。那就换一个思路。优先队列这个思路中，重复操作了 orders 次，其实在这些操作中，有一些是没有必要的废操作。这些大量的“废”操作导致了超时。试想，在 orders 次操作中，能否合并 n 个 pop 操作，一口气先 pop 掉 n 个前 n 大的数呢？这个是可行的，因为每次 pop 出去，元素都只会减一，这个是非常有规律的。

• 为了接下来的描述更加清晰易懂，还需要再定义 1 个值， thresholdValue 为操作 n 次以后，当前 inventory 数组的最大值。关于 thresholdValue 的理解，这里要说明一下。 thresholdValue 的来源有 2 种，一种是本来数组里面就有这个值，还有一种来源是 inventory[i] 元素减少到了 thresholdValue 这个值。举个例子：原始数组是 [2,3,3,4,5]，orders = 4，取 4 次以后，剩下的数组是 [2,2,3,3,3]。3 个 3 里面其中一个 3 就来自于 4-1=3，或者 5-2=3。

• 用二分搜索在 [0，max(inventory)] 区间内找到这个 thresholdValue 值，能满足下列不等式的最小 thresholdValue 值： \[ \sum_{inventory[i]\geqslant thresholdValue}^{} \left ( inventory[i] - thresholdValue \right )\leqslant orders \] thresholdValue 越小，不等式左边的值越大，随着 thresholdValue 的增大，不等式左边的值越来越小，直到刚刚能小于等于 orders。求出了 thresholdValue 值以后，还需要再判断有多少值等于 thresholdValue - 1 值了。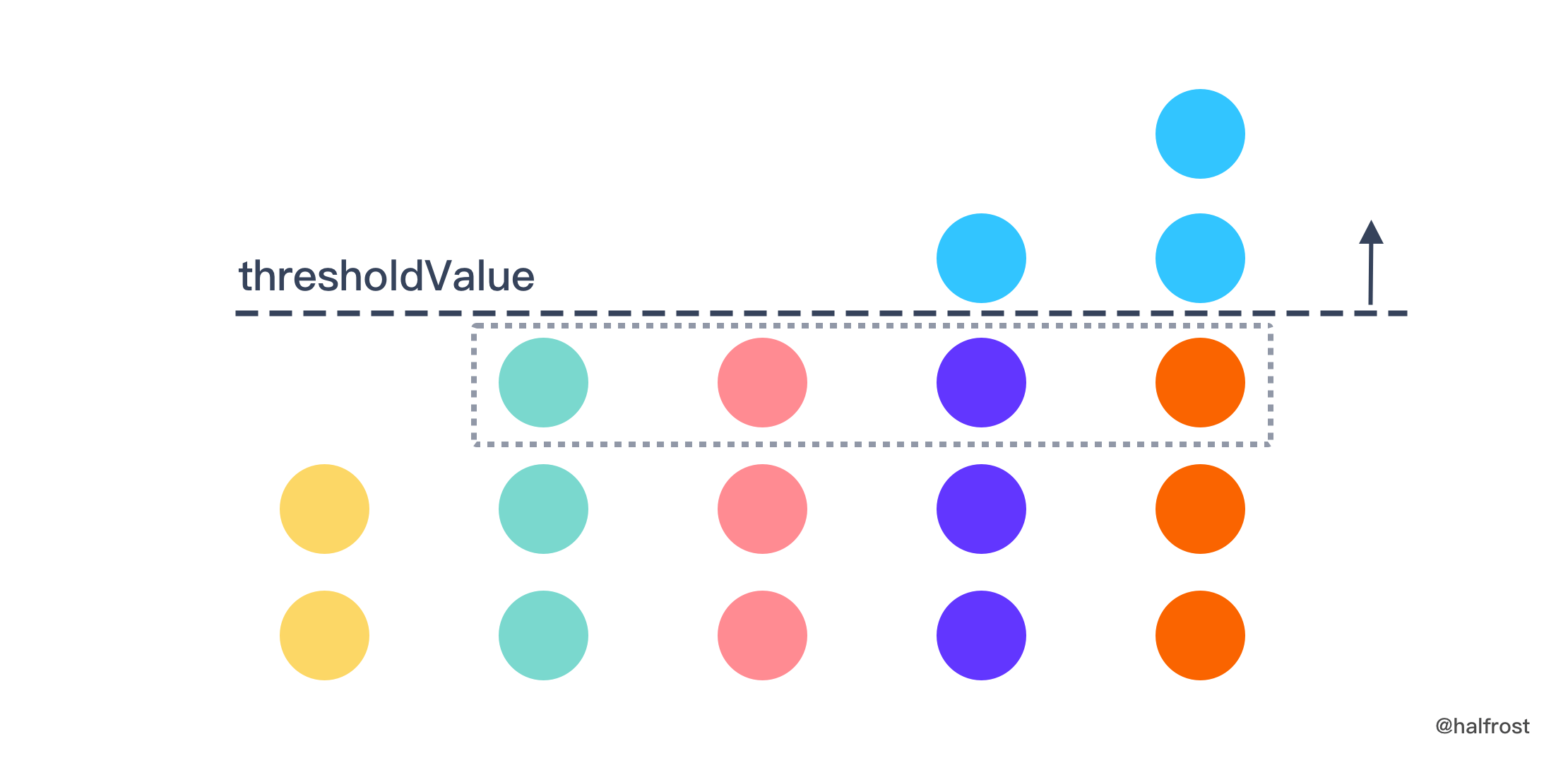

  

• 还是举上面的例子，原始数组是 [2,3,3,4,5]，orders = 4，我们可以求得 thresholdValue = 3 。inventory[i] > thresholdValue 的那部分 100% 的要取走，thresholdValue 就像一个水平面，突出水平面的那些都要拿走，每列的值按照等差数列求和公式计算即可。但是 orders - thresholdValue = 1，说明水平面以下还要拿走一个，即 thresholdValue 线下的虚线框里面的那 4 个球，还需要任意取走一个。最后总的结果是这 2 部分的总和，( ( 5 + 4 ) + 4 ) + 3 = 16 。

代码 #

package leetcode

import (
	"container/heap"
)

// 解法一 贪心 + 二分搜索
func maxProfit(inventory []int, orders int) int {
	maxItem, thresholdValue, count, res, mod := 0, -1, 0, 0, 1000000007
	for i := 0; i < len(inventory); i++ {
		if inventory[i] > maxItem {
			maxItem = inventory[i]
		}
	}
	low, high := 0, maxItem
	for low <= high {
		mid := low + ((high - low) >> 1)
		for i := 0; i < len(inventory); i++ {
			count += max(inventory[i]-mid, 0)
		}
		if count <= orders {
			thresholdValue = mid
			high = mid - 1
		} else {
			low = mid + 1
		}
		count = 0
	}
	count = 0
	for i := 0; i < len(inventory); i++ {
		count += max(inventory[i]-thresholdValue, 0)
	}
	count = orders - count
	for i := 0; i < len(inventory); i++ {
		if inventory[i] >= thresholdValue {
			if count > 0 {
				res += (thresholdValue + inventory[i]) * (inventory[i] - thresholdValue + 1) / 2
				count--
			} else {
				res += (thresholdValue + 1 + inventory[i]) * (inventory[i] - thresholdValue) / 2
			}
		}
	}
	return res % mod
}