1659. Maximize Grid Happiness #

题目 #

You are given four integers, m, n, introvertsCount, and extrovertsCount. You have an m x n grid, and there are two types of people: introverts and extroverts. There are introvertsCount introverts and extrovertsCount extroverts.

You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you do not have to have all the people living in the grid.

The happiness of each person is calculated as follows:

Introverts start with 120 happiness and lose 30 happiness for each neighbor (introvert or extrovert).
Extroverts start with 40 happiness and gain 20 happiness for each neighbor (introvert or extrovert).

Neighbors live in the directly adjacent cells north, east, south, and west of a person’s cell.

The grid happiness is the sum of each person’s happiness. Return the maximum possible grid happiness.

Example 1:

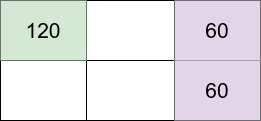
Input: m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
Output: 240
Explanation: Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).
- Introvert at (1,1) happiness: 120 (starting happiness) - (0 * 30) (0 neighbors) = 120
- Extrovert at (1,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
- Extrovert at (2,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
The grid happiness is 120 + 60 + 60 = 240.
The above figure shows the grid in this example with each person's happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.

Example 2:

Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
Output: 260
Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).
- Introvert at (1,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
- Extrovert at (2,1) happiness: 40 (starting happiness) + (2 * 20) (2 neighbors) = 80
- Introvert at (3,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
The grid happiness is 90 + 80 + 90 = 260.

Example 3:

Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
Output: 240

Constraints:

1 <= m, n <= 5
0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

题目大意 #

给你四个整数 m、n、introvertsCount 和 extrovertsCount 。有一个 m x n 网格，和两种类型的人：内向的人和外向的人。总共有 introvertsCount 个内向的人和 extrovertsCount 个外向的人。请你决定网格中应当居住多少人，并为每个人分配一个网格单元。注意，不必让所有人都生活在网格中。每个人的幸福感计算如下：

内向的人开始时有 120 个幸福感，但每存在一个邻居（内向的或外向的）他都会失去 30 个幸福感。
外向的人开始时有 40 个幸福感，每存在一个邻居（内向的或外向的）他都会得到 20 个幸福感。

邻居是指居住在一个人所在单元的上、下、左、右四个直接相邻的单元中的其他人。网格幸福感是每个人幸福感的总和。返回最大可能的网格幸福感。

解题思路 #

给出 m x n 网格和两种人，要求如何安排这两种人能使得网格的得分最大。两种人有各自的初始分，相邻可能会加分也有可能减分。
这一题状态很多。首先每个格子有 3 种状态，那么每一行有 3^6 = 729 种不同的状态。每行行内分数变化值可能是 -60(两个内向)，+40(两个外向)，-10(一个内向一个外向)。两行行间分数变化值可能是 -60(两个内向)，+40(两个外向)，-10(一个内向一个外向)。那么我们可以把每行的状态压缩成一个三进制，那么网格就变成了一维，每两个三进制之间的关系是行间关系，每个三进制内部还需要根据内向和外向的人数决定行内最终分数。定义 dp[lineStatusLast][row][introvertsCount][extrovertsCount] 代表在上一行 row - 1 的状态是 lineStatusLast 的情况下，当前枚举到了第 row 行，内向还有 introvertsCount 个人，外向还有 extrovertsCount 个人能获得的最大分数。状态转移方程是 dp[lineStatusLast(row-1)][row][introvertsCount][extrovertsCount] = max{dp[lineStatusLast(row)][row+1][introvertsCount - countIC(lineStatusLast(row)) ][extrovertsCount - countEC(lineStatusLast(row)) ] + scoreInner(lineStatusLast(row)) + scoreOuter(lineStatusLast(row-1),lineStatusLast(row))} ，这里有 2 个统计函数，countIC 是统计当前行状态三进制里面有多少个内向人。countEC 是统计当前行状态三进制里面有多少个外向人。scoreInner 是计算当前行状态三进制的行内分数。scoreOuter 是计算 row -1 行和 row 行之间的行间分数。
由于这个状态转移方程的计算量是巨大的。所以需要预先初始化一些计算结果。比如把 729 中行状态分别对应的行内、行间的分数都计算好，在动态规划状态转移的时候，直接查表获取分数即可。这样我们在深搜的时候，利用 dp 的记忆化，可以大幅减少时间复杂度。
题目中还提到，人数可以不用完。如果 introvertsCount = 0, extrovertsCount = 0 ，即人数都用完了的情况，这时候 dp = 0。如果 row = m，即已经枚举完了所有行，那么不管剩下多少人，这一行的 dp = 0 。
初始化的时候，注意，特殊处理 0 的情况，0 行 0 列都初始化为 -1 。

代码 #

package leetcode

import (
	"math"
)

func getMaxGridHappiness(m int, n int, introvertsCount int, extrovertsCount int) int {
	// lineStatus 					将每一行中 3 种状态进行编码，空白 - 0，内向人 - 1，外向人 - 2，每行状态用三进制表示
	// lineStatusList[729][6] 		每一行的三进制表示
	// introvertsCountInner[729] 	每一个 lineStatus 包含的内向人数
	// extrovertsCountInner[729] 	每一个 lineStatus 包含的外向人数
	// scoreInner[729] 			 	每一个 lineStatus 包含的行内得分（只统计 lineStatus 本身的得分，不包括它与上一行的）
	// scoreOuter[729][729] 	 	每一个 lineStatus 包含的行外得分
	// dp[上一行的 lineStatus][当前处理到的行][剩余的内向人数][剩余的外向人数]
	n3, lineStatus, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter, lineStatusList, dp := math.Pow(3.0, float64(n)), 0, [729]int{}, [729]int{}, [729]int{}, [729][729]int{}, [729][6]int{}, [729][6][7][7]int{}
	for i := 0; i < 729; i++ {
		lineStatusList[i] = [6]int{}
	}
	for i := 0; i < 729; i++ {
		dp[i] = [6][7][7]int{}
		for j := 0; j < 6; j++ {
			dp[i][j] = [7][7]int{}
			for k := 0; k < 7; k++ {
				dp[i][j][k] = [7]int{-1, -1, -1, -1, -1, -1, -1}
			}
		}
	}
	// 预处理
	for lineStatus = 0; lineStatus < int(n3); lineStatus++ {
		tmp := lineStatus
		for i := 0; i < n; i++ {
			lineStatusList[lineStatus][i] = tmp % 3
			tmp /= 3
		}
		introvertsCountInner[lineStatus], extrovertsCountInner[lineStatus], scoreInner[lineStatus] = 0, 0, 0
		for i := 0; i < n; i++ {
			if lineStatusList[lineStatus][i] != 0 {
				// 个人分数
				if lineStatusList[lineStatus][i] == 1 {
					introvertsCountInner[lineStatus]++
					scoreInner[lineStatus] += 120
				} else if lineStatusList[lineStatus][i] == 2 {
					extrovertsCountInner[lineStatus]++
					scoreInner[lineStatus] += 40
				}
				// 行内分数
				if i-1 >= 0 {
					scoreInner[lineStatus] += closeScore(lineStatusList[lineStatus][i], lineStatusList[lineStatus][i-1])
				}
			}
		}
	}
	// 行外分数
	for lineStatus0 := 0; lineStatus0 < int(n3); lineStatus0++ {
		for lineStatus1 := 0; lineStatus1 < int(n3); lineStatus1++ {
			scoreOuter[lineStatus0][lineStatus1] = 0
			for i := 0; i < n; i++ {
				scoreOuter[lineStatus0][lineStatus1] += closeScore(lineStatusList[lineStatus0][i], lineStatusList[lineStatus1][i])
			}
		}
	}
	return dfs(0, 0, introvertsCount, extrovertsCount, m, int(n3), &dp, &introvertsCountInner, &extrovertsCountInner, &scoreInner, &scoreOuter)
}

// 如果 x 和 y 相邻，需要加上的分数
func closeScore(x, y int) int {
	if x == 0 || y == 0 {
		return 0
	}
	// 两个内向的人，每个人要 -30，一共 -60
	if x == 1 && y == 1 {
		return -60
	}
	if x == 2 && y == 2 {
		return 40
	}
	return -10
}

// dfs(上一行的 lineStatus，当前处理到的行，剩余的内向人数，剩余的外向人数）
func dfs(lineStatusLast, row, introvertsCount, extrovertsCount, m, n3 int, dp *[729][6][7][7]int, introvertsCountInner, extrovertsCountInner, scoreInner *[729]int, scoreOuter *[729][729]int) int {
	// 边界条件：如果已经处理完，或者没有人了
	if row == m || introvertsCount+extrovertsCount == 0 {
		return 0
	}
	// 记忆化
	if dp[lineStatusLast][row][introvertsCount][extrovertsCount] != -1 {
		return dp[lineStatusLast][row][introvertsCount][extrovertsCount]
	}
	best := 0
	for lineStatus := 0; lineStatus < n3; lineStatus++ {
		if introvertsCountInner[lineStatus] > introvertsCount || extrovertsCountInner[lineStatus] > extrovertsCount {
			continue
		}
		score := scoreInner[lineStatus] + scoreOuter[lineStatus][lineStatusLast]
		best = max(best, score+dfs(lineStatus, row+1, introvertsCount-introvertsCountInner[lineStatus], extrovertsCount-extrovertsCountInner[lineStatus], m, n3, dp, introvertsCountInner, extrovertsCountInner, scoreInner, scoreOuter))
	}
	dp[lineStatusLast][row][introvertsCount][extrovertsCount] = best
	return best
}

func max(a int, b int) int {
	if a > b {
		return a
	}
	return b
}

⬅️上一页

下一页➡️