1691. Maximum Height by Stacking Cuboids #

题目 #

Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid’s dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

Example 1:

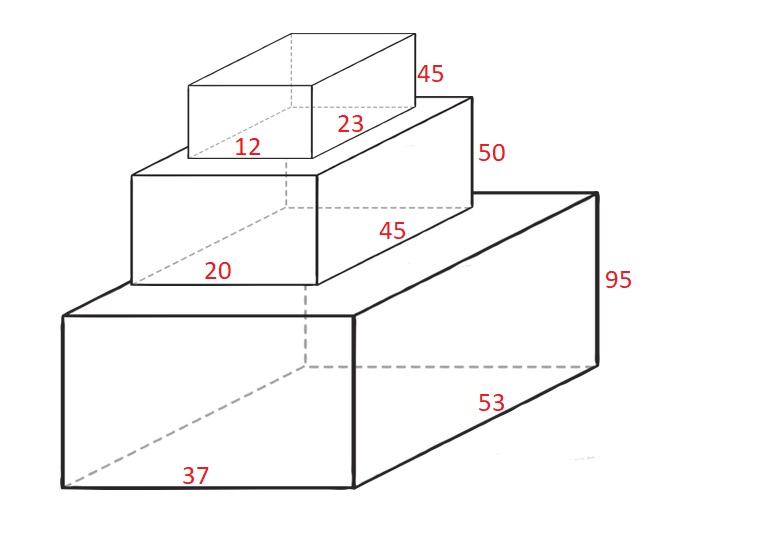
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

Constraints:

• n == cuboids.length
• 1 <= n <= 100
• 1 <= widthi, lengthi, heighti <= 100

题目大意 #

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个 子集 ，并将它们堆叠起来。如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。返回 堆叠长方体 cuboids 可以得到的 最大高度 。

解题思路 #

• 这一题是 LIS 最长递增子序列系列问题的延续。一维 LIS 问题是第 300 题。二维 LIS 问题是 354 题。这一题是三维的 LIS 问题。
• 题目要求最终摞起来的长方体尽可能的高，那么把长宽高中最大的值旋转为高。这是针对单个方块的排序。多个方块间还要排序，因为他们摞起来有要求，大的方块必须放在下面。所以针对多个方块，按照长，宽，高的顺序进行排序。两次排序完成以后，可以用动态规划找出最大值了。定义 dp[i] 为以 i 为最后一块砖块所能堆叠的最高高度。由于长和宽已经排好序了。所以只需要在 [0, i - 1] 这个区间内动态更新 dp 最大值。

代码 #

package leetcode

import "sort"

func maxHeight(cuboids [][]int) int {
	n := len(cuboids)
	for i := 0; i < n; i++ {
		sort.Ints(cuboids[i]) // 立方体三边内部排序
	}
	// 立方体排序，先按最短边，再到最长边
	sort.Slice(cuboids, func(i, j int) bool {
		if cuboids[i][0] != cuboids[j][0] {
			return cuboids[i][0] < cuboids[j][0]
		}
		if cuboids[i][1] != cuboids[j][1] {
			return cuboids[i][1] < cuboids[j][1]
		}
		return cuboids[i][2] < cuboids[j][2]
	})
	res := 0
	dp := make([]int, n)
	for i := 0; i < n; i++ {
		dp[i] = cuboids[i][2]
		res = max(res, dp[i])
	}
	for i := 1; i < n; i++ {
		for j := 0; j < i; j++ {
			if cuboids[j][0] <= cuboids[i][0] && cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] {
				dp[i] = max(dp[i], dp[j]+cuboids[i][2])
			}
		}
		res = max(res, dp[i])
	}
	return res
}

func max(x, y int) int {
	if x > y {
		return x
	}
	return y
}