线段树 Segment Tree #

线段树 Segment tree 是一种二叉树形数据结构，1977年由 Jon Louis Bentley 发明，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。

一个包含 \(n \) 个区间的线段树，空间复杂度为 \( O(n) \) ，查询的时间复杂度则为 \(O(log n+k) \) ，其中 \( k \) 是符合条件的区间数量。线段树的数据结构也可推广到高维度。

一. 什么是线段树 #

以一维的线段树为例。

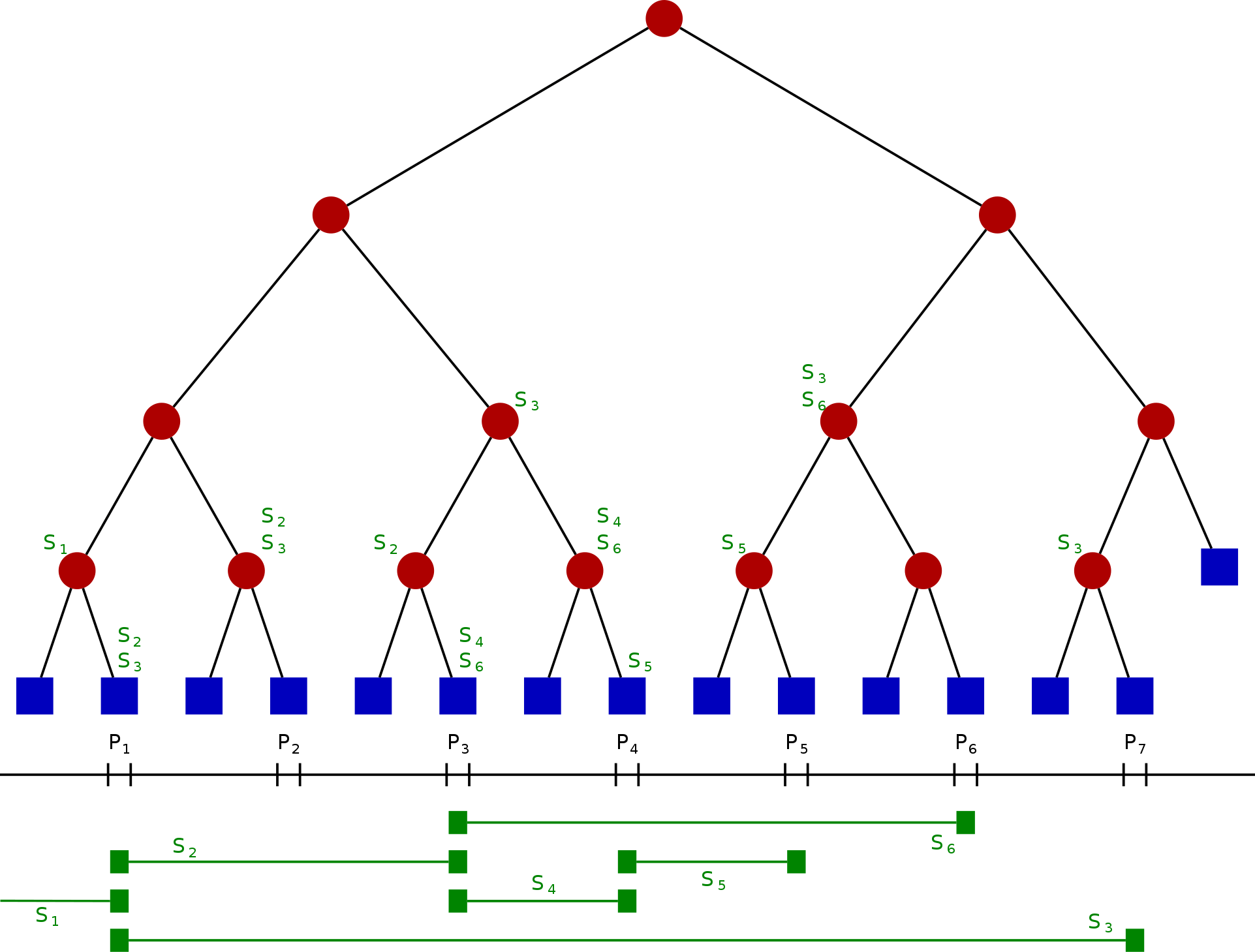
令 S 是一维线段的集合。将这些线段的端点坐标由小到大排序，令其为 \(x_{1},x_{2},\cdots ,x_{m} \) 。我们将被这些端点切分的每一个区间称为“单位区间”（每个端点所在的位置会单独成为一个单位区间），从左到右包含：

\[ (-\infty ,x_{1}),[x_{1},x_{1}],(x_{1},x_{2}),[x_{2},x_{2}],...,(x_{m-1},x_{m}),[x_{m},x_{m}],(x_{m},+\infty )\]

线段树的结构为一个二叉树，每个节点都代表一个坐标区间，节点 N 所代表的区间记为 Int(N)，则其需符合以下条件：

其每一个叶节点，从左到右代表每个单位区间。
其内部节点代表的区间是其两个儿子代表的区间之并集。
每个节点（包含叶子）中有一个存储线段的数据结构。若一个线段 S 的坐标区间包含 Int(N) 但不包含 Int(parent(N))，则节点 N 中会存储线段 S。

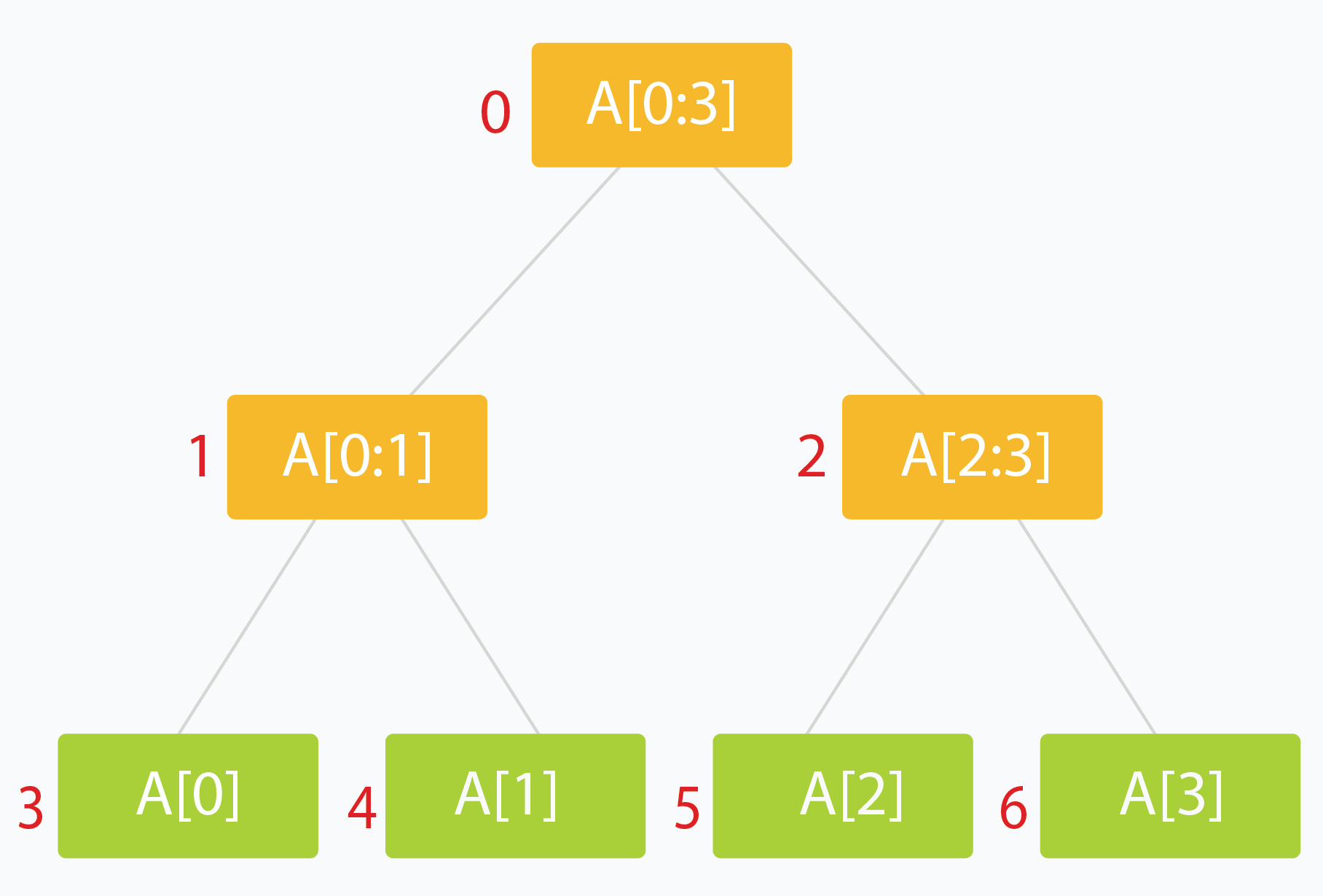
线段树是二叉树，其中每个节点代表一个区间。通常，一个节点将存储一个或多个合并的区间的数据，以便可以执行查询操作。

二. 为什么需要这种数据结构 #

许多问题要求我们基于对可用数据范围或区间的查询来给出结果。这可能是一个繁琐而缓慢的过程，尤其是在查询数量众多且重复的情况下。线段树让我们以对数时间复杂度有效地处理此类查询。

线段树可用于计算几何和地理信息系统领域。例如，距中心参考点/原点一定距离的空间中可能会有大量点。假设我们要查找距原点一定距离范围内的点。一个普通的查找表将需要对所有可能的点或所有可能的距离进行线性扫描（假设是散列图）。线段树使我们能够以对数时间实现这一需求，而所需空间却少得多。这样的问题称为平面范围搜索。有效地解决此类问题至关重要，尤其是在处理动态数据且瞬息万变的情况下（例如，用于空中交通的雷达系统）。下文会以线段树解决 Range Sum Query problem 为例。

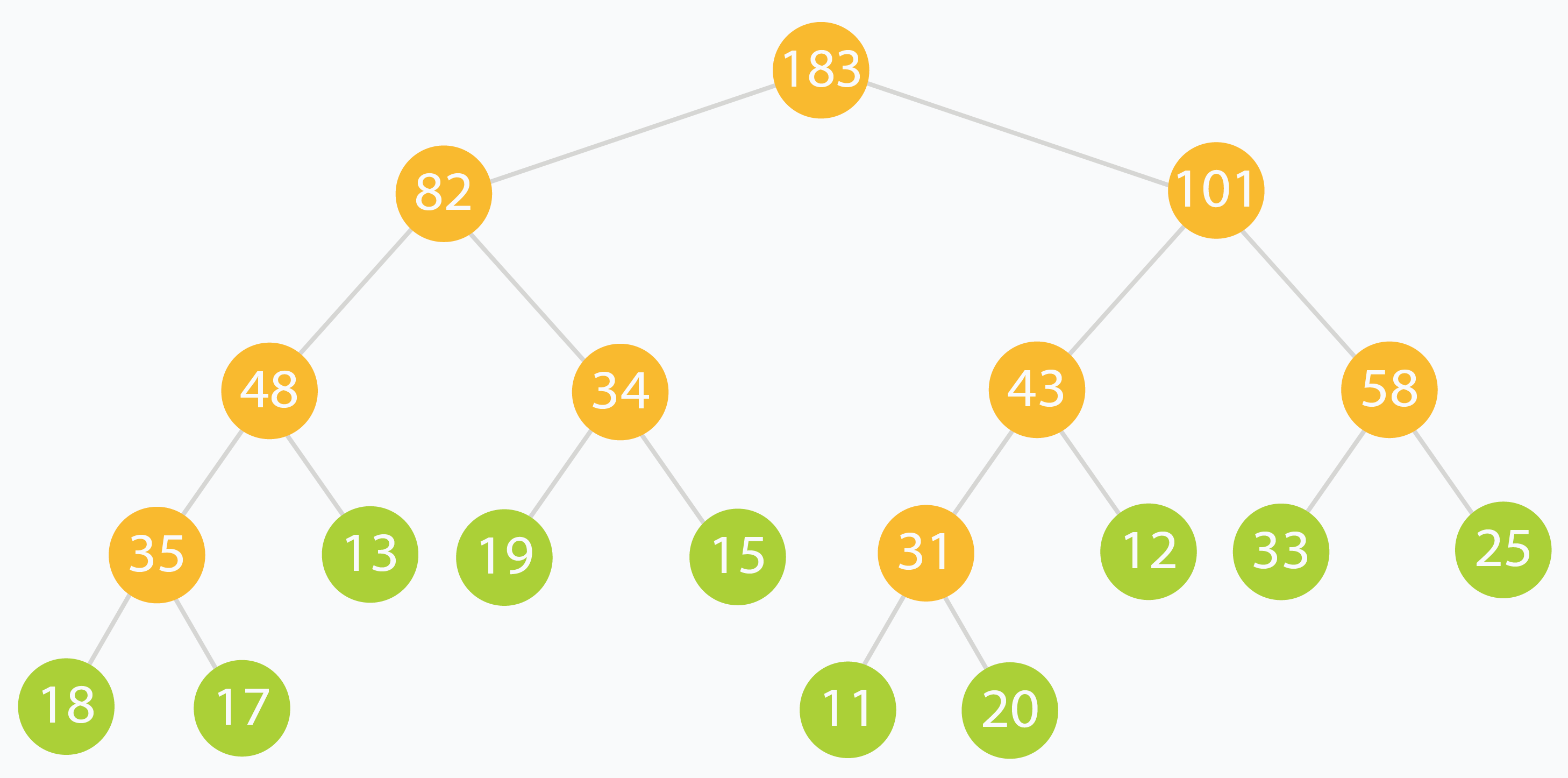
上图即作为范围查询的线段树。

三. 构造线段树 #

假设数据存在 size 为 n 的 arr[] 中。

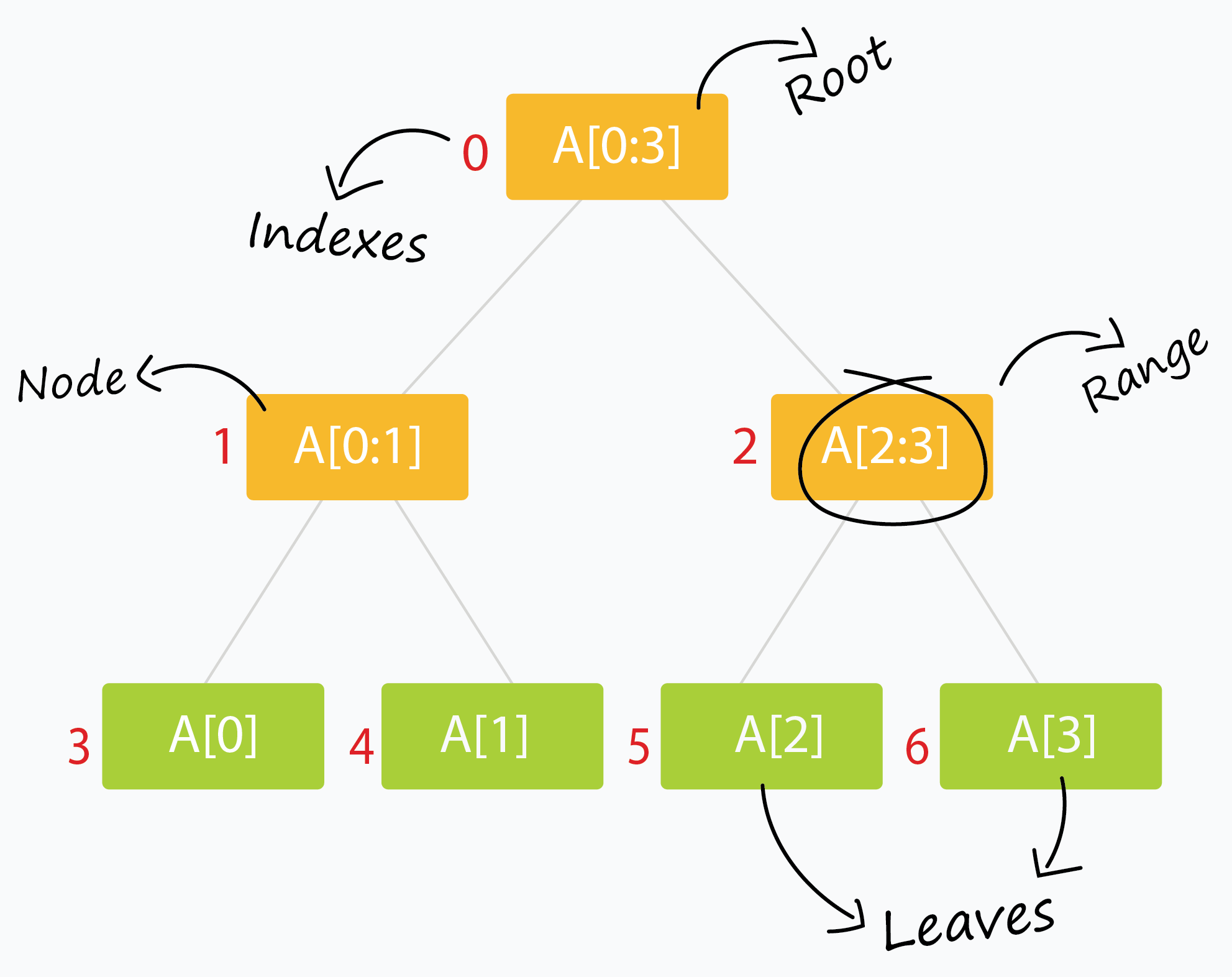
线段树的根通常代表整个数据区间。这里是 arr[0：n-1]。
树的每个叶子代表一个范围，其中仅包含一个元素。因此，叶子代表 arr[0]，arr[1] 等等，直到 arr[n-1]。
树的内部节点将代表其子节点的合并或并集结果。
每个子节点可代表其父节点所代表范围的大约一半。(二分的思想)

使用大小为 \(\approx 4 \ast n \) 的数组可以轻松表示 n 个元素范围的线段树。（ Stack Overflow 对原因进行了很好的讨论。如果你还不确定，请不要担心。本文将在稍后进行讨论。）

下标为 i 的节点有两个节点，下标分别为 \((2 \ast i + 1) \) 和 \((2 \ast i + 2)\) 。

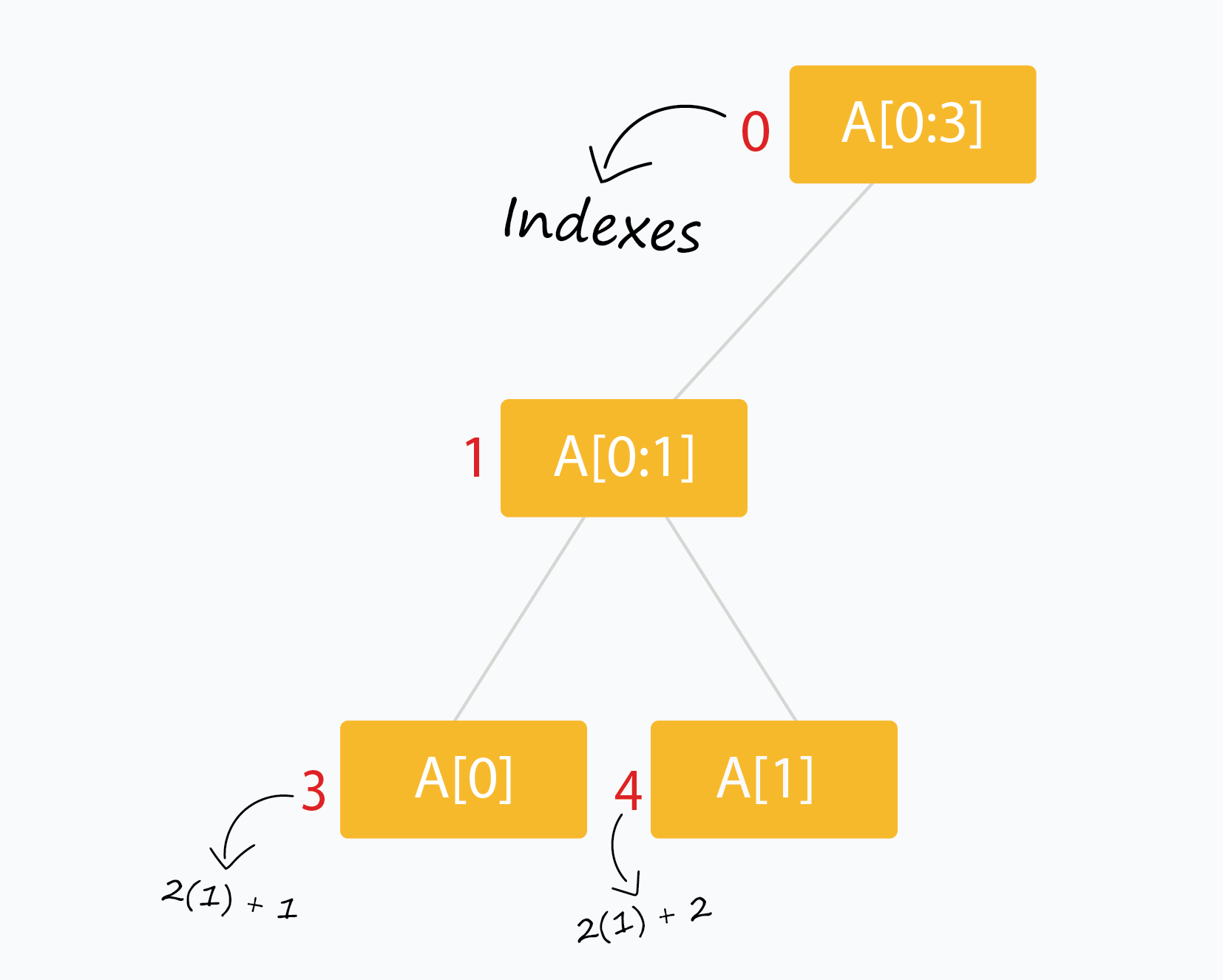
线段树看上去很直观并且非常适合递归构造。

我们将使用数组 tree[] 来存储线段树的节点（初始化为全零）。下标从 0 开始。

树的节点在下标 0 处。因此 tree[0] 是树的根。
tree[i] 的孩子存在 tree[2 * i + 1] 和 tree[2 * i + 2] 中。
用额外的 0 或 null 值填充 arr[]，使得 \(n = 2^{k} \) （其中 n 是 arr[] 的总长度，而 k 是非负整数。）
叶子节点的下标取值范围在 \( \in [2^{k}-1, 2^{k+1}-2]\)

构造线段树的代码如下：

// SegmentTree define
type SegmentTree struct {
	data, tree, lazy []int
	left, right      int
	merge            func(i, j int) int
}

// Init define
func (st *SegmentTree) Init(nums []int, oper func(i, j int) int) {
	st.merge = oper
	data, tree, lazy := make([]int, len(nums)), make([]int, 4*len(nums)), make([]int, 4*len(nums))
	for i := 0; i < len(nums); i++ {
		data[i] = nums[i]
	}
	st.data, st.tree, st.lazy = data, tree, lazy
	if len(nums) > 0 {
		st.buildSegmentTree(0, 0, len(nums)-1)
	}
}

// 在 treeIndex 的位置创建 [left....right] 区间的线段树
func (st *SegmentTree) buildSegmentTree(treeIndex, left, right int) {
	if left == right {
		st.tree[treeIndex] = st.data[left]
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	st.buildSegmentTree(leftTreeIndex, left, midTreeIndex)
	st.buildSegmentTree(rightTreeIndex, midTreeIndex+1, right)
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

func (st *SegmentTree) leftChild(index int) int {
	return 2*index + 1
}

func (st *SegmentTree) rightChild(index int) int {
	return 2*index + 2
}

笔者将线段树合并的操作变成了一个函数。合并操作根据题意变化，常见的有加法，取 max，min 等等。

我们以 arr[] = [18, 17, 13, 19, 15, 11, 20, 12, 33, 25 ] 为例构造线段树：

线段树构造好以后，数组里面的数据是：

tree[] = [ 183, 82, 101, 48, 34, 43, 58, 35, 13, 19, 15, 31, 12, 33, 25, 18, 17, 0, 0, 0, 0, 0, 0, 11, 20, 0, 0, 0, 0, 0, 0 ]

线段树用 0 填充到 4*n 个元素。

LeetCode 对应题目是 218. The Skyline Problem、 303. Range Sum Query - Immutable、 307. Range Sum Query - Mutable、 699. Falling Squares

四. 线段树的查询 #

线段树的查询方法有两种，一种是直接查询，另外一种是懒查询。

1. 直接查询 #

当查询范围与当前节点表示的范围完全匹配时，该方法返回结果。否则，它会更深入地遍历线段树树，以找到与节点的一部分完全匹配的节点。

// 查询 [left....right] 区间内的值

// Query define
func (st *SegmentTree) Query(left, right int) int {
	if len(st.data) > 0 {
		return st.queryInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

// 在以 treeIndex 为根的线段树中 [left...right] 的范围里，搜索区间 [queryLeft...queryRight] 的值
func (st *SegmentTree) queryInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	if left == queryLeft && right == queryRight {
		return st.tree[treeIndex]
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if queryLeft > midTreeIndex {
		return st.queryInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight)
	} else if queryRight <= midTreeIndex {
		return st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
	}
	return st.merge(st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, midTreeIndex),
		st.queryInTree(rightTreeIndex, midTreeIndex+1, right, midTreeIndex+1, queryRight))
}

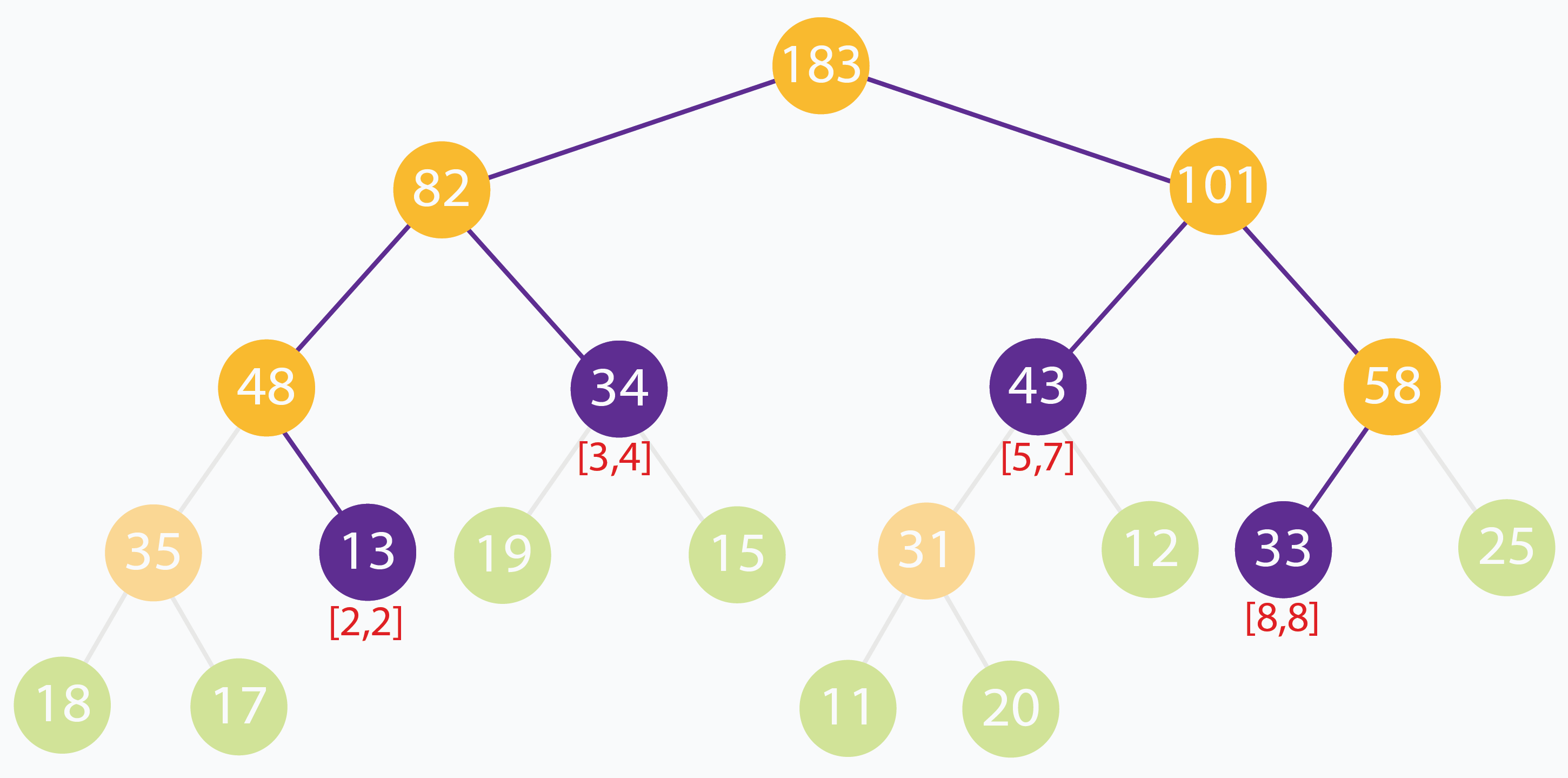
在上面的示例中，查询的区间范围为[2，8] 的元素之和。没有任何线段可以完全代表[2，8] 范围。但是可以观察到，可以使用范围 [2，2]，[3，4]，[5，7]，[8，8] 这 4 个区间构成 [8，8]。快速验证 [2,8] 处的输入元素之和为 13 + 19 + 15 + 11 + 20 + 12 + 33 = 123。[2，2]，[3，4]，[5，7] 和 [8，8] 的节点总和是 13 + 34 + 43 + 33 = 123。答案正确。

2. 懒查询 #

懒查询对应懒更新，两者是配套操作。在区间更新时，并不直接更新区间内所有节点，而是把区间内节点增减变化的值存在 lazy 数组中。等到下次查询的时候再把增减应用到具体的节点上。这样做也是为了分摊时间复杂度，保证查询和更新的时间复杂度在 O(log n) 级别，不会退化成 O(n) 级别。

懒查询节点的步骤：

先判断当前节点是否是懒节点。通过查询 lazy[i] 是否为 0 判断。如果是懒节点，将它的增减变化应用到该节点上。并且更新它的孩子节点。这一步和更新操作的第一步完全一样。
递归查询子节点，以找到适合的查询节点。

具体代码如下：

// 查询 [left....right] 区间内的值

// QueryLazy define
func (st *SegmentTree) QueryLazy(left, right int) int {
	if len(st.data) > 0 {
		return st.queryLazyInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

func (st *SegmentTree) queryLazyInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if left > queryRight || right < queryLeft { // segment completely outside range
		return 0 // represents a null node
	}
	if st.lazy[treeIndex] != 0 { // this node is lazy
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], st.lazy[treeIndex])
			// st.tree[treeIndex] += (right - left + 1) * st.lazy[treeIndex] // normalize current node by removing lazinesss
		}
		if left != right { // update lazy[] for children nodes
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], st.lazy[treeIndex])
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], st.lazy[treeIndex])
			// st.lazy[leftTreeIndex] += st.lazy[treeIndex]
			// st.lazy[rightTreeIndex] += st.lazy[treeIndex]
		}
		st.lazy[treeIndex] = 0 // current node processed. No longer lazy
	}
	if queryLeft <= left && queryRight >= right { // segment completely inside range
		return st.tree[treeIndex]
	}
	if queryLeft > midTreeIndex {
		return st.queryLazyInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight)
	} else if queryRight <= midTreeIndex {
		return st.queryLazyInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
	}
	// merge query results
	return st.merge(st.queryLazyInTree(leftTreeIndex, left, midTreeIndex, queryLeft, midTreeIndex),
		st.queryLazyInTree(rightTreeIndex, midTreeIndex+1, right, midTreeIndex+1, queryRight))
}

五. 线段树的更新 #

1. 单点更新 #

单点更新类似于 buildSegTree。更新树的叶子节点的值，该值与更新后的元素相对应。这些更新的值会通过树的上层节点把影响传播到根。

// 更新 index 位置的值

// Update define
func (st *SegmentTree) Update(index, val int) {
	if len(st.data) > 0 {
		st.updateInTree(0, 0, len(st.data)-1, index, val)
	}
}

// 以 treeIndex 为根，更新 index 位置上的值为 val
func (st *SegmentTree) updateInTree(treeIndex, left, right, index, val int) {
	if left == right {
		st.tree[treeIndex] = val
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if index > midTreeIndex {
		st.updateInTree(rightTreeIndex, midTreeIndex+1, right, index, val)
	} else {
		st.updateInTree(leftTreeIndex, left, midTreeIndex, index, val)
	}
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

在此示例中，下标为（在原始输入数据中）1、3 和 6 处的元素分别增加了 +3，-1 和 +2。可以看到更改如何沿树传播，一直到根。

2. 区间更新 #

线段树仅更新单个元素，非常有效，时间复杂度 O(log n)。但是，如果我们要更新一系列元素怎么办？按照当前的方法，每个元素都必须独立更新，每个元素都会花费一些时间。分别更新每一个叶子节点意味着要多次处理它们的共同祖先。祖先节点可能被更新多次。如果想要减少这种重复计算，该怎么办？

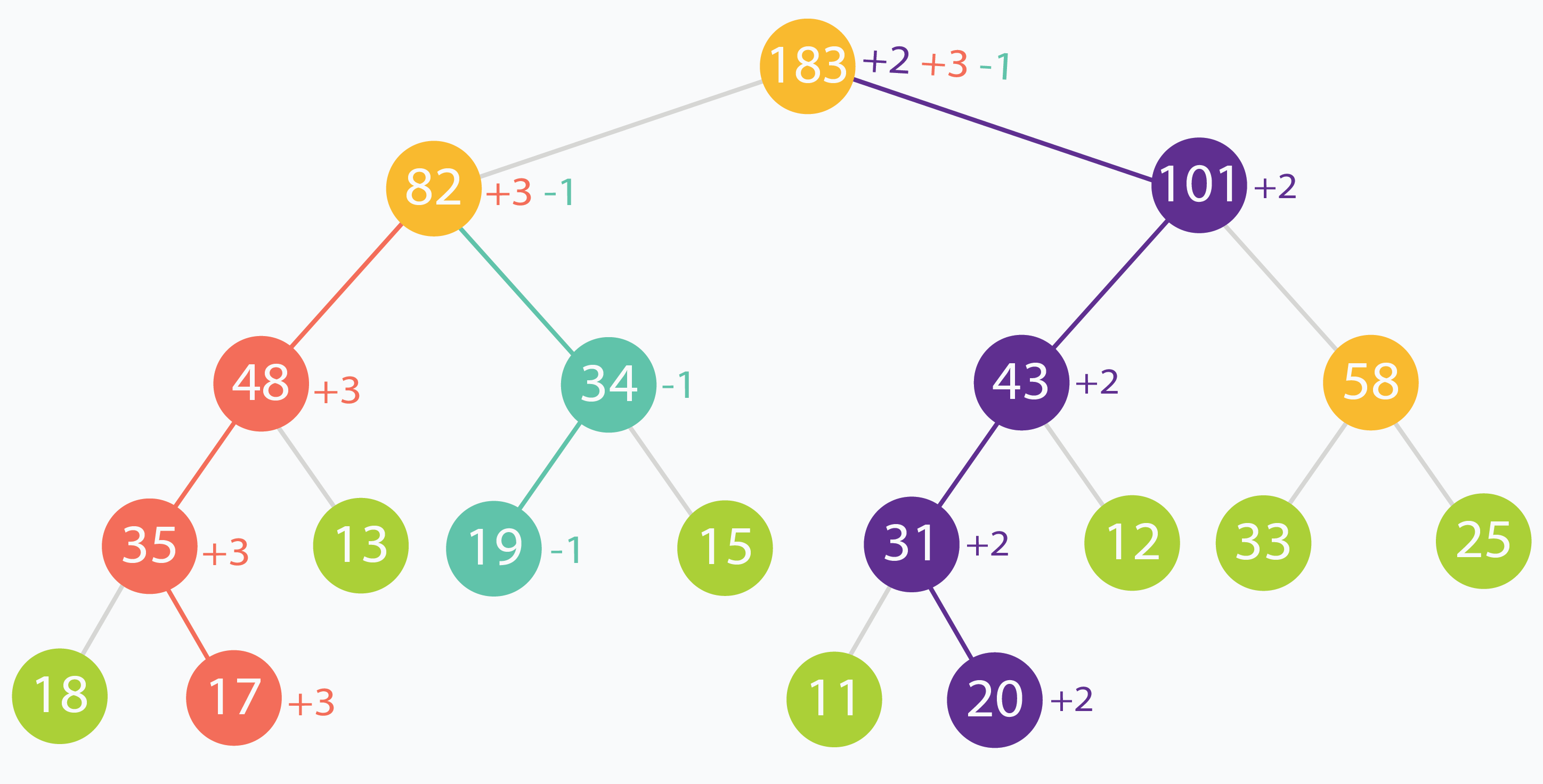
在上面的示例中，根节点被更新了三次，而编号为 82 的节点被更新了两次。这是因为更新叶子节点对上层父亲节点有影响。最差的情况，查询的区间内不包含频繁更新的元素，于是需要花费很多时间更新不怎么访问的节点。增加额外的 lazy 数组，可以减少不必要的计算，并且能按需处理节点。

使用另一个数组 lazy[]，它的大小与我们的线段树 array tree[] 完全相同，代表一个惰性节点。当访问或查询该节点时，lazy[i] 中保留需要增加或者减少该节点 tree[i] 的数量。当 lazy[i] 为 0 时，表示 tree[i] 该节点不是惰性的，并且没有缓存的更新。

更新区间内节点的步骤：

先判断当前节点是否是懒节点。通过查询 lazy[i] 是否为 0 判断。如果是懒节点，将它的增减变化应用到该节点上。并且更新它的孩子节点。
如果当前节点代表的区间位于更新范围内，则将当前更新操作应用于当前节点。
递归更新子节点。

具体代码如下：


// 更新 [updateLeft....updateRight] 位置的值
// 注意这里的更新值是在原来值的基础上增加或者减少，而不是把这个区间内的值都赋值为 x，区间更新和单点更新不同
// 这里的区间更新关注的是变化，单点更新关注的是定值
// 当然区间更新也可以都更新成定值，如果只区间更新成定值，那么 lazy 更新策略需要变化，merge 策略也需要变化，这里暂不详细讨论

// UpdateLazy define
func (st *SegmentTree) UpdateLazy(updateLeft, updateRight, val int) {
	if len(st.data) > 0 {
		st.updateLazyInTree(0, 0, len(st.data)-1, updateLeft, updateRight, val)
	}
}

func (st *SegmentTree) updateLazyInTree(treeIndex, left, right, updateLeft, updateRight, val int) {
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if st.lazy[treeIndex] != 0 { // this node is lazy
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], st.lazy[treeIndex])
			//st.tree[treeIndex] += (right - left + 1) * st.lazy[treeIndex] // normalize current node by removing laziness
		}
		if left != right { // update lazy[] for children nodes
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], st.lazy[treeIndex])
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], st.lazy[treeIndex])
			// st.lazy[leftTreeIndex] += st.lazy[treeIndex]
			// st.lazy[rightTreeIndex] += st.lazy[treeIndex]
		}
		st.lazy[treeIndex] = 0 // current node processed. No longer lazy
	}

	if left > right || left > updateRight || right < updateLeft {
		return // out of range. escape.
	}

	if updateLeft <= left && right <= updateRight { // segment is fully within update range
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], val)
			//st.tree[treeIndex] += (right - left + 1) * val // update segment
		}
		if left != right { // update lazy[] for children
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], val)
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], val)
			// st.lazy[leftTreeIndex] += val
			// st.lazy[rightTreeIndex] += val
		}
		return
	}
	st.updateLazyInTree(leftTreeIndex, left, midTreeIndex, updateLeft, updateRight, val)
	st.updateLazyInTree(rightTreeIndex, midTreeIndex+1, right, updateLeft, updateRight, val)
	// merge updates
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

LeetCode 对应题目是 218. The Skyline Problem、 699. Falling Squares

六. 时间复杂度分析 #

让我们看一下构建过程。我们访问了线段树的每个叶子（对应于数组 arr[] 中的每个元素）。因此，我们处理大约 2 * n 个节点。这使构建过程时间复杂度为 O(n)。对于每个递归更新的过程都将丢弃区间范围的一半，以到达树中的叶子节点。这类似于二分搜索，只需要对数时间。更新叶子后，将更新树的每个级别上的直接祖先。这花费时间与树的高度成线性关系。

4*n 个节点可以确保将线段树构建为完整的二叉树，从而树的高度为 log(4*n + 1) 向上取整。线段树读取和更新的时间复杂度都为 O(log n)。

七. 常见题型 #

1. Range Sum Queries #

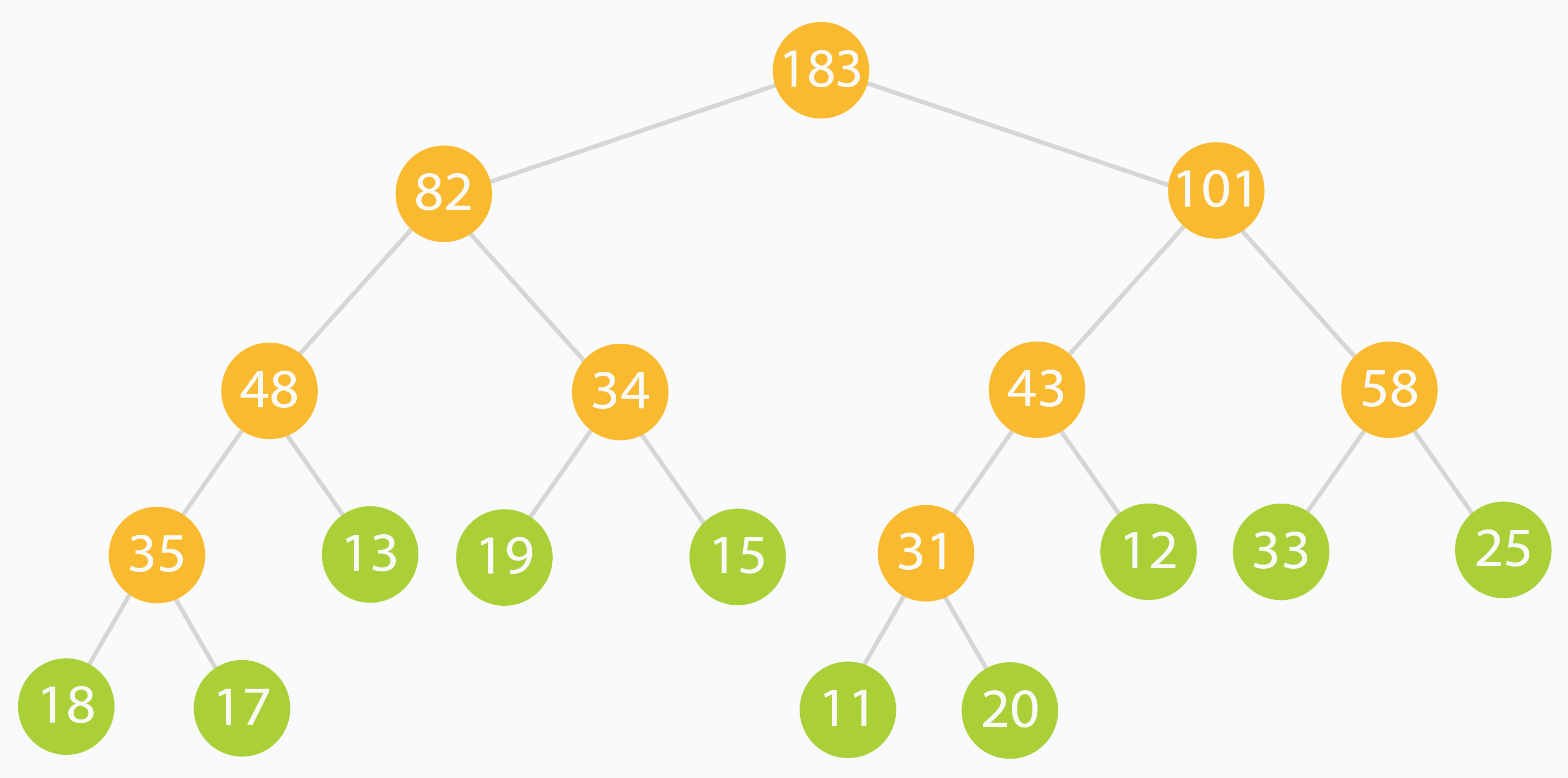
Range Sum Queries 是 Range Queries 问题的子集。给定一个数据元素数组或序列，需要处理由元素范围组成的读取和更新查询。线段树 Segment Tree 和树状数组 Binary Indexed Tree (a.k.a. Fenwick Tree)) 都能很快的解决这类问题。

Range Sum Query 问题专门处理查询范围内的元素总和。这个问题存在许多变体，包括不可变数据，可变数据，多次更新，单次查询和多次更新，多次查询。

2. 单点更新 #

HDU 1166 敌兵布阵 update:单点增减 query:区间求和
HDU 1754 I Hate It update:单点替换 query:区间最值
HDU 1394 Minimum Inversion Number update:单点增减 query:区间求和
HDU 2795 Billboard query:区间求最大值的位子(直接把update的操作在query里做了)

3. 区间更新 #

HDU 1698 Just a Hook update:成段替换 (由于只query一次总区间,所以可以直接输出 1 结点的信息)
POJ 3468 A Simple Problem with Integers update:成段增减 query:区间求和
POJ 2528 Mayor’s posters 离散化 + update:成段替换 query:简单hash
POJ 3225 Help with Intervals update:成段替换,区间异或 query:简单hash

4. 区间合并 #

这类题目会询问区间中满足条件的连续最长区间,所以PushUp的时候需要对左右儿子的区间进行合并

POJ 3667 Hotel update:区间替换 query:询问满足条件的最左端点

5. 扫描线 #

这类题目需要将一些操作排序,然后从左到右用一根扫描线扫过去最典型的就是矩形面积并,周长并等题

HDU 1542 Atlantis update:区间增减 query:直接取根节点的值
HDU 1828 Picture update:区间增减 query:直接取根节点的值

6. 计数问题 #

在 LeetCode 中还有一类问题涉及到计数的。 315. Count of Smaller Numbers After Self， 327. Count of Range Sum， 493. Reverse Pairs 这类问题可以用下面的套路解决。线段树的每个节点存的是区间计数。

// SegmentCountTree define
type SegmentCountTree struct {
	data, tree  []int
	left, right int
	merge       func(i, j int) int
}

// Init define
func (st *SegmentCountTree) Init(nums []int, oper func(i, j int) int) {
	st.merge = oper

	data, tree := make([]int, len(nums)), make([]int, 4*len(nums))
	for i := 0; i < len(nums); i++ {
		data[i] = nums[i]
	}
	st.data, st.tree = data, tree
}

// 在 treeIndex 的位置创建 [left....right] 区间的线段树
func (st *SegmentCountTree) buildSegmentTree(treeIndex, left, right int) {
	if left == right {
		st.tree[treeIndex] = st.data[left]
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	st.buildSegmentTree(leftTreeIndex, left, midTreeIndex)
	st.buildSegmentTree(rightTreeIndex, midTreeIndex+1, right)
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

func (st *SegmentCountTree) leftChild(index int) int {
	return 2*index + 1
}

func (st *SegmentCountTree) rightChild(index int) int {
	return 2*index + 2
}

// 查询 [left....right] 区间内的值

// Query define
func (st *SegmentCountTree) Query(left, right int) int {
	if len(st.data) > 0 {
		return st.queryInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

// 在以 treeIndex 为根的线段树中 [left...right] 的范围里，搜索区间 [queryLeft...queryRight] 的值，值是计数值
func (st *SegmentCountTree) queryInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	if queryRight < st.data[left] || queryLeft > st.data[right] {
		return 0
	}
	if queryLeft <= st.data[left] && queryRight >= st.data[right] || left == right {
		return st.tree[treeIndex]
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	return st.queryInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight) +
		st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
}

// 更新计数

// UpdateCount define
func (st *SegmentCountTree) UpdateCount(val int) {
	if len(st.data) > 0 {
		st.updateCountInTree(0, 0, len(st.data)-1, val)
	}
}

// 以 treeIndex 为根，更新 [left...right] 区间内的计数
func (st *SegmentCountTree) updateCountInTree(treeIndex, left, right, val int) {
	if val >= st.data[left] && val <= st.data[right] {
		st.tree[treeIndex]++
		if left == right {
			return
		}
		midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
		st.updateCountInTree(rightTreeIndex, midTreeIndex+1, right, val)
		st.updateCountInTree(leftTreeIndex, left, midTreeIndex, val)
	}
}

⬅️上一页

下一页➡️